
| a1(1-qn) |
| 1-q |
| q |
| 1+q2 |
| 1 |
| 2 |
| q |
| 1+q2 |
| 1 |
| 2 |
| 1 |
| 2 |


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
| 方案 | 类别 | 基本费用 | 超时费用 |
| 甲 | 包月制(不限时) | 130元 | 无 |
| 乙 | 有限包月制(限60小时) | 80元 | 3元/小时 |
| 18n+642 |
| 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
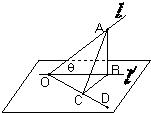 如图,l是平面α的斜线,斜足是O,A是l上任意一点,AB是平面α的垂线,B是垂足,设OD是平面α内与OB不同的一条直线,AC垂直于OD于C,若直线l与平面α所成的角θ=45°,∠BOC=45°,求∠AOC的大小.
如图,l是平面α的斜线,斜足是O,A是l上任意一点,AB是平面α的垂线,B是垂足,设OD是平面α内与OB不同的一条直线,AC垂直于OD于C,若直线l与平面α所成的角θ=45°,∠BOC=45°,求∠AOC的大小.查看答案和解析>>
科目:高中数学 来源: 题型:
| A、{0,1,2,3,4,5,6} |
| B、{0,1,3,4,5,6} |
| C、{0,1,2,3,5,6} |
| D、{0,1,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、-2 | B、0 |
| C、2 | D、与x有关的一个值 |
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
直线 与函数
与函数
 的图象恰有三个公共点,则实数
的图象恰有三个公共点,则实数 的取值范围是( )
的取值范围是( )
(A)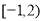 (B)
(B) (C)
(C)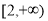 (D)
(D)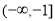
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com