Question

13．已知函数f（x）=$\left\{\begin{array}{l}{{e}^{x}，x≤0}\\{{x}^{2}-2x+1，x＞0}\end{array}\right.$，则方程f²（x）-3f（x）+2=0的根的个数是（　　）

• A． 3
• B． 4
• C． 5
• D． 6

Answer 1

分析 求解方程f²（x）-3f（x）+2=0，得f（x）=1或f（x）=2，画出函数f（x）=$\left\{\begin{array}{l}{{e}^{x}，x≤0}\\{{x}^{2}-2x+1，x＞0}\end{array}\right.$的图象，数形结合得答案．

解答 解：由f²（x）-3f（x）+2=0，得f（x）=1或f（x）=2．
画出函数f（x）=$\left\{\begin{array}{l}{{e}^{x}，x≤0}\\{{x}^{2}-2x+1，x＞0}\end{array}\right.$的图象如图：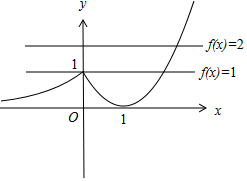

由图可知，方程f（x）=1有1根，方程f（x）=2有2根．
∴方程f²（x）-3f（x）+2=0的根的个数是3．
故选：A．

点评 本题考查根的存在性及根的个数判断，考查数学转化思想方法与数形结合的解题思想方法，是中档题．