
【题目】设函数![]() .
.
(1)若![]() 时,
时,![]() 取得极值,求
取得极值,求![]() 的值;
的值;
(2)若![]() 在其定义域内为增函数,求
在其定义域内为增函数,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)先求函数的导函数,根据若![]() 时,
时,![]() 取得极值得
取得极值得![]() ,解之即可;(2)
,解之即可;(2)![]() 在其定义域内为增函数可转化成只需在
在其定义域内为增函数可转化成只需在![]() 内有
内有![]() 恒成立,根据二次函数的图象与性质建立不等式关系,解之即可.
恒成立,根据二次函数的图象与性质建立不等式关系,解之即可.
试题解析:![]()
(1)因为![]() 时,
时,![]() 取得极值,所以
取得极值,所以![]() ,
,
即![]() 故
故![]() .
.
(2)![]() 的定义域为
的定义域为![]() .方程
.方程![]() 的判别式
的判别式![]() ,
,
(Ⅰ) 当![]() , 即
, 即![]() 时,
时,![]() ,
,
![]() 在
在![]() 内恒成立, 此时
内恒成立, 此时![]() 为增函数.
为增函数.
(Ⅱ)当![]() , 即
, 即![]() 或
或![]() 时,
时,
要使![]() 在定义域
在定义域![]() 内为增函数, 只需在
内为增函数, 只需在![]() 内有
内有![]() 即可,
即可,
设![]() ,
,
由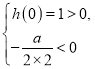 得
得 ![]() , 所以
, 所以![]() .
.
由(1) (2)可知,若![]() 在其定义域内为增函数,
在其定义域内为增函数,![]() 的取值范围是
的取值范围是![]() .
.
【方法点晴】本题主要考查利用导数研究函数的极值以及利用单调性求参数的范围,属于中档题. 利用单调性求参数的范围的常见方法:① 视参数为已知数,依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较求参数需注意若函数在区间![]() 上是单调的,则该函数在此区间的任意子集上也是单调的; ② 利用导数转化为不等式
上是单调的,则该函数在此区间的任意子集上也是单调的; ② 利用导数转化为不等式![]() 或
或![]() 恒成立问题求参数范围,本题(2)是利用方法 ② 求解的.
恒成立问题求参数范围,本题(2)是利用方法 ② 求解的.


科目:高中数学 来源: 题型:
【题目】为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查. 得到如下的统计结果.
表1:男生上网时间与频数分布表:
上网时间(分钟) |
|
|
|
|
|
人数 | 10 | 20 | 40 | 20 | 10 |
表2:女生上网时间与频数分布表:
上网时间(分钟) |
|
|
|
|
|
人数 | 5 | 25 | 30 | 25 | 15 |
完成下面的2×2列联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”?


附: ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用水清洗一份蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用1个单位量的水可洗掉蔬菜上残留农药量的![]() ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用![]() 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数![]() .
.
(1)求![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(2)现有![]() 单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知五边形ABECD由一个直角梯形![]() 和一个等边三角形
和一个等边三角形![]() 构成(如图1所示),
构成(如图1所示),![]() 且
且![]() .将梯形
.将梯形![]() 沿着
沿着![]() 折起(如图2所示),点
折起(如图2所示),点![]() 是
是![]() 的中点,
的中点,![]() 平面
平面![]()
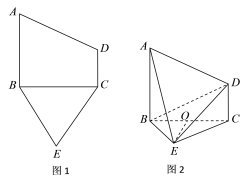
(1)求证:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2![]() sin(3ωx
sin(3ωx![]() ),其中ω>0.
),其中ω>0.
(1)若f(x+θ)是最小周期为2π的偶函数,求ω和θ的值;
(2)若f(x)在(0,![]() ]上是增函数,求ω的最大值.
]上是增函数,求ω的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为[0,1])的函数f(x),如果同时满足以下三条:①对任意的x∈[0,1],总有f(x)≥0;②f (1)=1;③若x1≥0,x2≥0,x1+x2≤1,都有f(x1+x2)≥f(x1)+f(x2)成立,则称函数f(x)为理想函数.
(1)判断函数g(x)=2x﹣1(x∈[0,1])是否为理想函数,并予以证明;
(2)若函数f(x)为理想函数,假定存在x0∈[0,1],使得f(x0)∈[0,1],且f(f(x0))=x0,求证f(x0)=x0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com