
 如图,在正三棱柱ABC-A1B1C1中,AB=4,AA1=6,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=4,AA1=6,E,F分别为BB1,AC的中点.分析 (1)如图,连接AC1交A1C于点O,连接OE,OF,可得OE⊥AC.OE⊥AA1.即OE⊥平面ACC1A1,于是平面A1EC⊥平面ACC1A1.
(2)几何体AA1EBC是四棱锥C-AA1EB,高为$h=4sin60°=2\sqrt{3}$,底面为直角梯形,面积为$S=\frac{1}{2}(3+6)×4=18$,利用体积公式求解.
解答 解:(1)如图,连接AC1交A1C于点O,连接OE,OF,在正三棱柱ABC-A1B1C1中,四边形ACC1A1为平行四边形,所以OA=OC1.
又因为F为AC中点,所以OF∥CC1且$OF=\frac{1}{2}C{C_1}$.
因为E为BB1中点,所以BE∥CC1且$BE=\frac{1}{2}C{C_1}$.
所以BE∥OF且BE=OF,
所以四边形BEOF是平行四边形,所以BF∥OE.
因为AB=CB,F为AC中点,所以BF⊥AC,所以可得OE⊥AC.
因为AA1⊥底面ABC,所以AA1⊥BF,所以可得OE⊥AA1.
又AA1,AC?平面ACC1A1,且AA1∩AC=A,所以OE⊥平面ACC1A1.
因为OE?平面A1EC,所以平面A1EC⊥平面ACC1A1.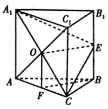
(2)几何体AA1EBC是四棱锥C-AA1EB,高为$h=4sin60°=2\sqrt{3}$,底面为直角梯形,面积为$S=\frac{1}{2}(3+6)×4=18$,
得${V_{{A_1}-B{B_1}{C_1}C}}=\frac{1}{3}×2\sqrt{3}×18=12\sqrt{3}$,
故几何体AA1EBC的体积为${V_{A{A_1}EBC}}=\frac{1}{2}×4×4×\frac{{\sqrt{3}}}{2}×6-12\sqrt{3}$=$12\sqrt{3}$.
点评 本题考查了空间面面垂直的判定,几何体的体积,属于中档题.


科目:高中数学 来源: 题型:选择题
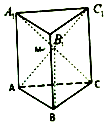 在三棱柱ABC-A1B1C1中,各侧面均为正方形,侧面AA1C1C的对角线相交于点M,则BM与平面ABC所成角的大小是( )
在三棱柱ABC-A1B1C1中,各侧面均为正方形,侧面AA1C1C的对角线相交于点M,则BM与平面ABC所成角的大小是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
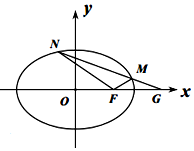 已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,直线$\frac{{\sqrt{2}}}{2}x+y=1$经过E的右顶点和上顶点.
已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,直线$\frac{{\sqrt{2}}}{2}x+y=1$经过E的右顶点和上顶点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
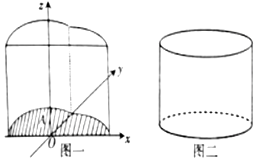 我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系xOy平面内,若函数f(x)=$\left\{\begin{array}{l}\sqrt{1-{x^2}},x∈[{-1,0})\\ cosx,x∈[{0,\frac{π}{2}}]\end{array}$的图象与x轴围成一个封闭的区域A,将区域A沿z轴的正方向平移4个单位,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域A的面积相等,则此圆柱的体积为π+4.
我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系xOy平面内,若函数f(x)=$\left\{\begin{array}{l}\sqrt{1-{x^2}},x∈[{-1,0})\\ cosx,x∈[{0,\frac{π}{2}}]\end{array}$的图象与x轴围成一个封闭的区域A,将区域A沿z轴的正方向平移4个单位,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域A的面积相等,则此圆柱的体积为π+4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com