
 ,其中
,其中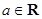 .
.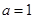 时,求曲线
时,求曲线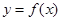 在原点处的切线方程;
在原点处的切线方程;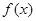 的单调区间.
的单调区间.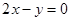
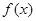 的单调增区间是
的单调增区间是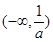 ,
,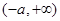 ;单调减区间是
;单调减区间是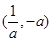
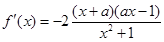
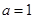 时,
时,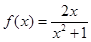 ,
,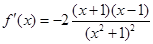 . ……………2分
. ……………2分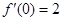 , 得曲线
, 得曲线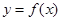 在原点处的切线方程是
在原点处的切线方程是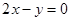 .………4分
.………4分 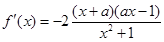 .……………5分
.……………5分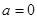 时,
时,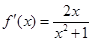 .
.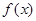 在
在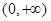 单调递增,在
单调递增,在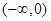 单调递减. ……7分
单调递减. ……7分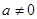 ,
,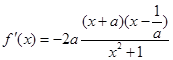 .
.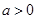 时,令
时,令 ,得
,得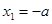 ,
,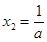 ,
,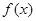 与
与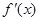 的情况如下:
的情况如下: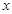 | 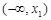 | 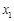 |  | 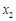 | 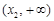 |
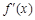 |  |  | 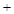 |  |  |
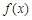 | ↘ | 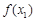 | ↗ | 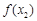 | ↘ |
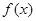 的单调减区间是
的单调减区间是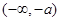 ,
,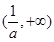 ;单调增区间是
;单调增区间是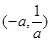 .…10分
.…10分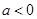 时,
时,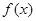 与
与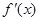 的情况如下:
的情况如下: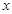 | 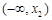 | 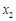 | 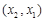 | 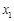 | 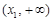 |
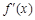 | 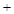 |  |  |  | 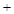 |
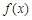 | ↗ | 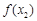 | ↘ | 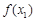 | ↗ |
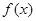 的单调增区间是
的单调增区间是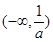 ,
,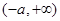 ;单调减区间是
;单调减区间是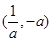 ………12分
………12分 

 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源:不详 题型:填空题
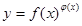 的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得 ,两边对
,两边对 求导数,得
求导数,得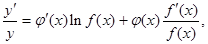 于是
于是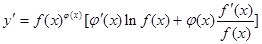 ,运用此方法可以求得函数
,运用此方法可以求得函数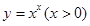 在(1,1)处的切线方程是 _________
在(1,1)处的切线方程是 _________查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
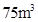 ,墙高为
,墙高为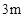 的长方体形的简易仓库. 已知仓库屋顶每平方米的造价为500元,墙壁每平方米的造价为400元,地面造价忽略不计. 问怎样设计仓库地面的长与宽,能使总造价最低?最低造价是多少?
的长方体形的简易仓库. 已知仓库屋顶每平方米的造价为500元,墙壁每平方米的造价为400元,地面造价忽略不计. 问怎样设计仓库地面的长与宽,能使总造价最低?最低造价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com