
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,满足
上的奇函数,满足![]() ,当
,当![]() 时,有
时,有![]() .
.
(1)求实数![]() 的值;
的值;
(2)求函数![]() 在区间
在区间![]() 上的解析式,并利用定义证明证明其在该区间上的单调性;
上的解析式,并利用定义证明证明其在该区间上的单调性;
(3)解关于![]() 的不等式
的不等式![]() .
.
【答案】(1)![]() ;(2)
;(2) ![]() ;详见解析(3)
;详见解析(3)![]()
【解析】
(1)根据![]() 是定义在
是定义在![]() 上的奇函数及
上的奇函数及![]() 时的
时的![]() 解析式即可得出
解析式即可得出![]() ,并可求出
,并可求出![]() ,从而可得出
,从而可得出![]() ,求出
,求出![]() ;(2)根据上面知,
;(2)根据上面知,![]() 时,
时,![]() ,从而可设
,从而可设![]() ,从而得出
,从而得出![]() ,从而得出
,从而得出![]() 时,
时,![]() ,再根据函数单调性的定义即可判断
,再根据函数单调性的定义即可判断![]() 在
在![]() 上的单调性.(3)不等式等价于
上的单调性.(3)不等式等价于![]() ,即
,即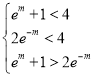 ,解不等式组即得解.
,解不等式组即得解.
(1)![]() 函数
函数![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,
![]() ,即
,即![]() ,
,![]() ,
,
又因为![]() (2)
(2)![]() ,所以
,所以![]() (2)
(2)![]() ,
,
即![]() ,所以
,所以![]() ,
,
综上可知![]() ,
,![]() .经检验满足题意.
.经检验满足题意.
(2)由(1)可知当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,且函数
,且函数![]() 是奇函数,
是奇函数,
![]()
![]() ,
,
![]() 当
当![]() 时,函数
时,函数![]() 的解析式为
的解析式为![]() ,
,
任取![]() ,
,![]() ,且
,且![]() ,则
,则![]() ,
,
![]() ,
,![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
于是![]() ,即
,即![]() ,
,
故![]() 在区间
在区间![]() 上是单调增函数;
上是单调增函数;
(3)![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,
,
![]() ,且
,且![]() 在
在![]() 上是增函数,
上是增函数,
![]()
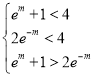 ,解得
,解得![]() ,
,
![]() 原不等式的解集为
原不等式的解集为![]() .
.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】给出下列三个命题,其中所有错误命题的序号是______.
![]() 抛物线
抛物线![]() 的准线方程为
的准线方程为![]() ;
;
![]() 过点
过点![]() 作与抛物线
作与抛物线![]() 只有一个公共点的直线t仅有1条;
只有一个公共点的直线t仅有1条;
![]() 是抛物线
是抛物线![]() 上一动点,以P为圆心作与抛物线准线相切的圆,则这个圆一定经过一个定点
上一动点,以P为圆心作与抛物线准线相切的圆,则这个圆一定经过一个定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某重点中学将全部高一新生分成A,B两个成绩相当(成绩的均值、方差都相同)的级部,A级部采用传统形式的教学方式,B级部采用新型的基于信息化的自主学习教学方式.期末考试后分别从两个级部中各随机抽取100名学生的数学成绩进行统计,得到如下数据:
A级部教学 成绩分组 |
|
|
|
|
|
|
频数 | 18 | 23 | 29 | 23 | 6 | 1 |
B级部教学 成绩分组 |
|
|
|
|
|
|
频数 | 8 | 16 | 24 | 28 | 21 | 3 |
若成绩不低于130分者为“优秀”.
根据上表数据分别估计A,B两个级部“优秀”的概率;
(2)填写下面的列联表,并根据列联表判断是否有99%的把握认为“优秀”与教学方式有关?
是否优秀 级部 | 优秀 | 不优秀 | 合计 |
A级部 | |||
B级部 | |||
合计 |
(3)根据上表数据完成下面的频率分布直方图,并根据频率分布直方图,分别求出A,B两个级部的中位数的估计值(精确到![]() );请根据以上计算结果初步分析A,B两个级部的教学成绩的优劣.
);请根据以上计算结果初步分析A,B两个级部的教学成绩的优劣.

附表:
|
|
|
|
|
|
|
|
|
|
|
|
附: 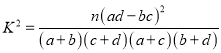
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游景点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每提高1元,租不出去的自行车就增加3辆.规定:每辆自行车的日租金不超过20元,每辆自行车的日租金![]() 元只取整数,并要求出租所有自行车一日的总收入必须超过一日的管理费用,用
元只取整数,并要求出租所有自行车一日的总收入必须超过一日的管理费用,用![]() 表示出租所有自行车的日净收入(即一日中出租所以自行车的总收入减去管理费用后的所得).
表示出租所有自行车的日净收入(即一日中出租所以自行车的总收入减去管理费用后的所得).
(1)求函数![]() 的解析式及定义域;
的解析式及定义域;
(2)试问日净收入最多时每辆自行车的日租金应定为多少元?日净收入最多为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】央视人民网报道:2019年7月15日,平顶山市文物管理局有关人士表示,郏县北大街古墓群抢救性发掘工作结束,共发现古墓539座,已发掘墓葬93座。该墓地是一处大型古墓群,在已发掘的93座墓葬中,有战国时期墓葬32座、两汉时期墓葬56座、唐墓2座、宋墓3座。生物体死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.检测一墓葬女尸出土时碳14的残余量约占原始含量的79%,则可推断为该墓葬属于( )时期(辅助数据:![]() )
)
参考时间轴:

A.战国B.两汉C.唐朝D.宋朝
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 上的动点
上的动点![]() 到坐标原点
到坐标原点![]() 的距离
的距离![]() 的最大值;
的最大值;
(Ⅱ)若曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆![]() 及其内接等腰三角形
及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转180°而成,如图2.已知圆
旋转180°而成,如图2.已知圆![]() 的半径为
的半径为![]() ,设
,设![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积![]() 最大.求
最大.求![]() 取得最大值时腰
取得最大值时腰![]() 的长度.
的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com