
【题目】【2018广东深圳市高三第一次调研考试】已知函数![]() .
.
(I)讨论函数![]() 的单调性;
的单调性;
(II)当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
【答案】(I)见解析;(II)![]() .
.
【解析】试题分析:(1)求出![]() 的定义域以及导函数
的定义域以及导函数![]() ,分四种情况讨论
,分四种情况讨论![]() 的范围,分别令
的范围,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)
的减区间;(2) ![]() ,等价于
,等价于![]() ,讨论
,讨论![]() 的范围,利用导数研究函数的单调性,分别令求出函数
的范围,利用导数研究函数的单调性,分别令求出函数![]() 的最小值,令最小值大于零,可筛选出符合题意的
的最小值,令最小值大于零,可筛选出符合题意的![]() 的取值范围.
的取值范围.
试题解析:(1) ![]() 的定义域为
的定义域为![]() .
.
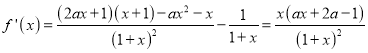 .
.
由![]() ,
, ![]() ,得
,得![]() ,
, ![]() .
.
①当![]() 时,
时, ![]() ,在
,在![]() 时,
时, ![]() ;在
;在![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 单调递减,
单调递减, ![]() 在
在![]() 单调递增;
单调递增;
②当![]() 时,
时, ![]() ,在
,在![]() 时,
时, ![]() ;在
;在![]() 时,
时, ![]() ;在
;在![]() 时,
时, ![]() .所以
.所以![]() 在
在![]() ,
, ![]() 单调递增,
单调递增, ![]() 在
在![]() 单调递减;
单调递减;
③当![]() 时,
时, ![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 单调递增;
单调递增;
④当![]() 时,
时, ![]() .在
.在![]() 时,
时, ![]() ;在
;在![]() 时,
时, ![]() ;在
;在![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() ,
, ![]() 单调递增,
单调递增, ![]() 在
在![]() 单调递减;
单调递减;
(2)当![]() 时,
时, ![]() ,
, ![]() ,即
,即![]() .
.
设![]() ,
, ![]() ,只需
,只需![]() ,在
,在![]() 上恒成立即可.
上恒成立即可.
因为![]() ,
, ![]() .
.
又![]() ,所以
,所以![]() .
.
令![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ,在
,在![]() 上
上![]() ,故
,故![]() 单调递增,
单调递增,
所以![]() 恒成立;
恒成立;
当![]() 时,
时, ![]() ,即
,即![]() ,故
,故![]() .
.
故当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,所以在
,所以在![]() 上
上![]() ,与题设矛盾.
,与题设矛盾.
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,所以在
,所以在![]() 上
上![]() ,与题设矛盾.
,与题设矛盾.
综上, ![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 设![]() ,则
,则![]() 为实数的充要条件是
为实数的充要条件是![]() 为共轭复数;
为共轭复数;
B. “直线![]() 与曲线C相切”是“直线
与曲线C相切”是“直线![]() 与曲线C只有一个公共点”的充分不必要条件;
与曲线C只有一个公共点”的充分不必要条件;
C. “若两直线![]() ,则它们的斜率之积等于
,则它们的斜率之积等于![]() ”的逆命题;
”的逆命题;
D. ![]() 是R上的可导函数,“若
是R上的可导函数,“若![]() 是
是![]() 的极值点,则
的极值点,则![]() ”的否命题.
”的否命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,满足
上的奇函数,满足![]() ,当
,当![]() 时,有
时,有![]() .
.
(1)求实数![]() 的值;
的值;
(2)求函数![]() 在区间
在区间![]() 上的解析式,并利用定义证明证明其在该区间上的单调性;
上的解析式,并利用定义证明证明其在该区间上的单调性;
(3)解关于![]() 的不等式
的不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校选派甲、乙、丙、丁、戊5名学生代表学校参加市级“演讲”和“诗词”比赛,下面是他们的一段对话.甲说:“乙参加‘演讲’比赛”;乙说:“丙参加‘诗词’比赛”;丙说“丁参加‘演讲’比赛”;丁说:“戊参加‘诗词’比赛”;戊说:“丁参加‘诗词’比赛”.
已知这5个人中有2人参加“演讲”比赛,有3人参加“诗词”比赛,其中有2人说的不正确,且参加“演讲”的2人中只有1人说的不正确.根据以上信息,可以确定参加“演讲”比赛的学生是
A. 甲和乙 B. 乙和丙 C. 丁和戊 D. 甲和丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国数学家科拉茨1937年提出一个著名的猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半(即
是偶数,就将它减半(即![]() );如果
);如果![]() 是奇数,则将它乘3加1(即
是奇数,则将它乘3加1(即![]() ),不断重复这样的运算,经过有限步后,一定可以得到1.对于科拉茨猜想,目前谁也不能证明,也不能否定.现在请你研究:如果对正整数
),不断重复这样的运算,经过有限步后,一定可以得到1.对于科拉茨猜想,目前谁也不能证明,也不能否定.现在请你研究:如果对正整数![]() (首项)按照上述规则进行变换后的第9项为1(注:1可以多次出现),则
(首项)按照上述规则进行变换后的第9项为1(注:1可以多次出现),则![]() 的所有不同值的个数为( )
的所有不同值的个数为( )
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量(百件)与销售单价x(元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.

(1)把y表示为x的函数;
(2)当销售价为每件50元时,该店正好收支平衡(即利润为零),求该店的职工人数;
(3)若该店只有20名职工,问销售单价定为多少元时,该专卖店可获得最大月利润?(注:利润=收入-支出)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com