
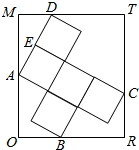
 如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.
如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3. 分析 以小正方形边的方向为坐标轴建立平面直角坐标系,求出各向量坐标,代入计算.
解答 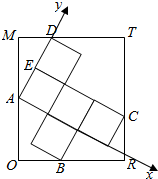 解:以A为坐标原点建立平面直角坐标系如图:
解:以A为坐标原点建立平面直角坐标系如图:
则A(0,0),E(0,$\sqrt{3}$),B(2$\sqrt{3}$,-$\sqrt{3}$),C(3$\sqrt{3}$,$\sqrt{3}$),D(0,2$\sqrt{3}$).
∴$\overrightarrow{AE}$=(0,$\sqrt{3}$),$\overrightarrow{BC}$=($\sqrt{3}$,2$\sqrt{3}$),$\overrightarrow{BD}$=(-2$\sqrt{3}$,3$\sqrt{3}$).
∴$\overrightarrow{AE}$-$\overrightarrow{BC}$=(-$\sqrt{3}$,-$\sqrt{3}$),
∴($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=6-9=-3.
故答案为-3.
点评 本题考查了平面向量的数量积运算,建立恰当的坐标系是解题关键.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,1) | B. | (-1,1] | C. | (-2,2) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2:1 | B. | 5:2 | C. | 1:4 | D. | 3:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
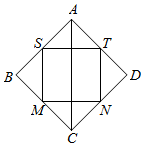 如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )
如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )| A. | 8:1 | B. | 2:1 | C. | 4:3 | D. | 8:3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
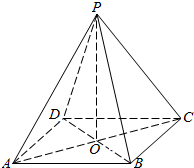 如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求:
如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com