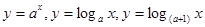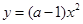练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图给出了函数,的图象，则与函数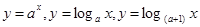,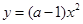依次对应的图象是（    ）
    A．①②③④B．①③②④
    C．②③①④D．①④③②
    B

    试题分析：从二次函数的抛物线形状，确定了开口向下，因此可知a-1<0,a<1,且a>0，故0<a<1,那么图像④是二次函数，排除D，然后再看在其定义域内都是减函数，分别的对应为①③，这样排除了选项A,C，而也可以通过底数是1<a+1<2，得到为增函数，对应②图像，故选B.
    点评：解决该试题的关键是找到问题的突破口，通过给定的函数类型,先确定出底数或者系数的范围，而最好的入手点就是以抛物线分析得到。因此对于数形结合的试题，要找好入手点很重要。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    已知函数，则         

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若函数y=f(x) (x∈R)满足：f(x+2)=f(x)，且x∈[–1, 1]时，f(x) =" |" x |，函数y=g(x)是定义在R上的奇函数，且x∈(0, +∞)时，g(x) =" log" 3 x，则函数y=f(x)的图像与函数y=g(x)的图像的交点个数为_______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

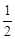    已知函数f(x)在(－1，1)上有定义，f()=－1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(－1,1)都有f(x)+f(y)=f(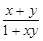),试证明：
    （1）f(x)为奇函数；
    （2）f(x)在(－1，1)上单调递减.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知实数，函数.
    （I）讨论在上的奇偶性；
    （II）求函数的单调区间；
    （III）求函数在闭区间上的最大值。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

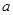    为了应对国际原油的变化，某地建设一座油料库。现在油料库已储油料吨，计划正式运营后的第一年进油量为已储油量的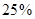，以后每年的进油量为上一年年底储油量的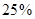，且每年运出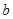吨，设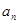为正式运营第n年年底的储油量。（其中）
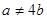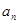    （1）求的表达式
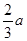    （2）为应对突发事件，该油库年底储油量不得少于吨，如果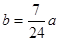吨，该油库能否长期按计划运营？如果可以请加以证明；如果不行请求出最多可以运营几年。（取）

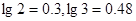    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设,则的值是（    ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    定义域为的函数有四个单调区间，则实数满足（ ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下列函数中既是偶函数又在（   ）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案