
分析 分类讨论,利用x1x2+y1y2=0,根据(1-k2)x2-4k2x-4k2-1=0,把两根的和与积代入后整理得到矛盾的式子,从而得到结论.
解答 解:当过M(-2,0)的直线l的斜率不存在时,直线l的方程为x=-2,
把x=-2代入双曲线x2-y2=1得,A(-2,$\sqrt{3}$),B(-2,-$\sqrt{3}$),此时不满足∠AOB=90°,
当过M(-2,0)的直线l的斜率存在时,设直线l的方程为y=k(x+2),
代入双曲线x2-y2=1,可得(1-k2)x2-4k2x-4k2-1=0,
设A(x1,y1),B(x2,y2),则x1+x2=$\frac{4{k}^{2}}{1-{k}^{2}}$,x1x2=-$\frac{4{k}^{2}+1}{1-4{k}^{2}}$,
若∠AOB=90°,则x1x2+y1y2=(k2+1)(-$\frac{4{k}^{2}+1}{1-4{k}^{2}}$)+2k2•$\frac{4{k}^{2}}{1-{k}^{2}}$+4k2=0
整理得,9k2+1=0.此式显然不成立.
所以,不存在使∠AOB=90°的直线l
点评 本题考查了直线与圆锥曲线的关系,直线与圆锥曲线的关系问题,常用“设而不求的”解题方法,即利用一元二次方程的根与系数关系求得直线与圆锥曲线的两个交点的横坐标的和与积,此题考查了分类讨论的数学思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{3}{2}}]$ | B. | $[{-\frac{3}{2},+∞})$ | C. | $[{-4,-\frac{3}{2}}]$ | D. | $[{-\frac{3}{2},1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
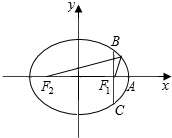 电影放映机上聚光灯泡的反射面,是由椭圆的一部分CAB(如图),绕着OA轴旋转而成的,如果把灯泡放在椭圆的一个焦点F1处,那么根据椭圆的光学性质,由F1发出光线,经反射面反射后,都集中在椭圆的另一个焦点F2处,因此,只要把影片放在F2处,就可以得到最强的光线,现已知|F1A|=1.5cm,|BC|=5.2cm,那么聚光灯泡F1与影片门F2之间应该距离多少cm.
电影放映机上聚光灯泡的反射面,是由椭圆的一部分CAB(如图),绕着OA轴旋转而成的,如果把灯泡放在椭圆的一个焦点F1处,那么根据椭圆的光学性质,由F1发出光线,经反射面反射后,都集中在椭圆的另一个焦点F2处,因此,只要把影片放在F2处,就可以得到最强的光线,现已知|F1A|=1.5cm,|BC|=5.2cm,那么聚光灯泡F1与影片门F2之间应该距离多少cm.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com