
分析 (1)利用有理数指数幂性质、运算法则求解.
(2)利用有理数、对数性质、运算法则、换底公式求解.
解答 解:(1)$a•\sqrt{\root{3}{a^4}•{a^3}•\root{3}{{{a^{-7}}}}}÷\root{3}{{\sqrt{{a^{-3}}}•{a^2}•\sqrt{a^5}}}$
=$a•{a}^{\frac{4}{6}}•{a}^{\frac{3}{2}}•{a}^{-\frac{7}{6}}$÷${a}^{-\frac{1}{2}}{a}^{\frac{2}{3}}{a}^{\frac{5}{6}}$
=a2÷a
=a.
(2)$\sqrt{\frac{9}{4}}-{(\frac{8}{27})^{-\frac{2}{3}}}+(lg5{)^2}+2lg2-{(lg2)^2}+({log_4}81)•({log_{27}}64)$
=$\frac{3}{2}-\frac{9}{4}$+(lg5)2+2lg2+(lg2)2+$\frac{lg81}{lg4}•\frac{lg64}{lg27}$
=$\frac{6}{4}-\frac{9}{4}+5$
=$\frac{17}{4}$.
点评 本题考查指数式、对数式化简求值,是基础题,解题时要认真审题,注意有理数、对数性质、运算法则、换底公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {2} | C. | {0,1,2,4,6} | D. | {0,2,3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
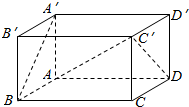 如图,长方体ABCD-A′B′C′D′中,AD=2AB=2AA′=2.
如图,长方体ABCD-A′B′C′D′中,AD=2AB=2AA′=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com