
| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 根据向量知识可知M为PF2的中点,结合${\overrightarrow{O{F}_{2}}}^{2}$=${\overrightarrow{{F}_{2}M}}^{2}$且2$\overrightarrow{O{F}_{2}}$•$\overrightarrow{{F}_{2}M}$=a2+b2可求出∠OF2M,从而得出M的坐标,再得出P点坐标,代入双曲线方程化简即可得出e.
解答 解:∵$\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{OP}+\overrightarrow{O{F}_{2}})$,∴M是PF2的中点,
∵${\overrightarrow{O{F}_{2}}}^{2}$=${\overrightarrow{{F}_{2}M}}^{2}$,∴OF2=F2M=c,
∴2$\overrightarrow{O{F}_{2}}$•$\overrightarrow{{F}_{2}M}$=2c2cos(π-∠OF2M)=a2+b2=c2,
∴∠OF2M=$\frac{2π}{3}$.
∴M($\frac{3c}{2}$,$\frac{\sqrt{3}c}{2}$),∵F2(c,0),M是PF2的中点,
∴P(2c,$\sqrt{3}$c),
∵P在双曲线上,$\frac{4{c}^{2}}{{a}^{2}}-\frac{3{c}^{2}}{{b}^{2}}=1$,即4b2c2-3a2c2-a2b2=0,
∵b2=c2-a2,∴4c2(c2-a2)-3a2c2-a2(c2-a2)=0,
即4c4-8a2c2+a4=0,
∵e=$\frac{c}{a}$,∴4e4-8e2+1=0,解得e2=1+$\frac{\sqrt{3}}{2}$或e2=1-$\frac{\sqrt{3}}{2}$(舍),
∴e=$\sqrt{1+\frac{\sqrt{3}}{2}}$=$\frac{1+\sqrt{3}}{2}$.
故选A.
点评 本题考查了双曲线的性质,平面向量的数量积运算,属于中档题.


 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|x≥2} | C. | {x|1≤x<2} | D. | {x|x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2) | B. | (1,2] | C. | [2,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
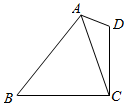 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,$cosB=\frac{{\sqrt{3}}}{3}$.
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,$cosB=\frac{{\sqrt{3}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 指数函数 | B. | 对数函数 | C. | 一次函数 | D. | 余弦函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com