练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

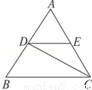
    （几何证明选讲选做题）如图3，△ABC中，D、E分别在边AB、AC上，CD平分∠ACB，DE∥BC，如果AC=10，AE=4，那么BC= ．

     

     

    15

    【解析】

    试题分析：先利用平行线的性质，再利用角平分线的性质，即可求得结论．

    【解析】
    ∵DE∥BC，AC=10，AE=4，

    ∴

    ∵CD平分∠ACB，

    ∴

    ∵AC=10

    ∴BC=15

    故答案为：15

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年北师大版必修三 1.1从普查到抽样练习卷（解析版） 题型：选择题

    从1008名学生中抽取20人参加义务劳动．规定采用下列方法选取：先用简单随机抽样的方法从1008人中剔除8人，剩下1000人再按系统抽样的方法抽取，那么这1008人中每个人入选的概率是（ ）

    A.都相等且等于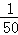

    B.都相等且等于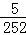

    C.不全相等

    D.均不相等

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修四4-1第一讲1.4练习卷（解析版） 题型：选择题

    如图，在矩形ABCD中，BD为对角线，AE⊥BD，，AD=1，则BE=（ ）

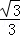    A.1 B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修四4-1第一讲1.2练习卷（解析版） 题型：选择题

    如图，在△ABC中，M是AC的中点，点E在AB上，且AE=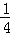AB，连接EM并延长交BC的延长线于点D，则BC：CD=（ ）

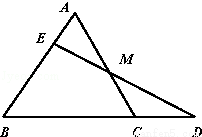
    A.2：1 B.3：1 C.3：2 D.4：1

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修四4-1第一讲1.2练习卷（解析版） 题型：选择题

    如图，AD是△ABC的中线，E在AC边上，AD交BE与F，若AE：EC=2：1，则AF：FD=（ ）

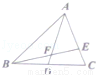
    A.2：1 B.3：1 C.4：1 D.5：1

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修四4-1第一讲1.1练习卷（解析版） 题型：填空题

    将边长为2，一个内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD，点E，F分别为AC，BD的中点，则下列命题中正确的是 ．

    ①EF∥AB；

    ②EF⊥BD；

    ③EF有最大值，无最小值；

    ④当四面体ABCD的体积最大时，；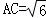

    ⑤AC垂直于截面BDE．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修四4-1第一讲1.1练习卷（解析版） 题型：选择题

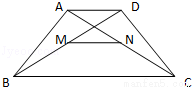
    已知，如图，在梯形ABCD中，AD∥BC，AD=3，BC=7，点M，N分别是对角线BD，AC的中点，则MN=（ ）

    A.2 B.5 C.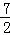 D.

     

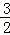
    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修一1-2第四章4.2练习卷（解析版） 题型：选择题

    如图是“集合”的知识结构图，如果要加入“子集”，则应该放在（ ）

    A.“集合的概念”的下位 B.“集合的表示”的下位

    C.“基本关系”的下位 D.“基本运算”的下位

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修一1-2第一章1.1练习卷（解析版） 题型：选择题

    （2014•呼和浩特一模）已知回归直线的斜率的估计值是1.23，样本点的中心为（4，5），则回归直线的方程是（ ）

    A.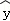=1.23x+4 B.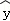=1.23x﹣0.08 C.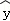=1.23x+0.8 D.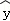=1.23x+0.08

     

    查看答案和解析>>

    同步练习册答案