练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】汕头某家电企业要将刚刚生产的100台变频空调送往市内某商场，现有4辆甲型货车和8辆乙型货车可供调配，每辆甲型货车的运输费用是400元，可装空调20台，每辆乙型货车的运输费用是300元，可装空调10台，若每辆车至多运一次，则企业所花的最少运费为（ ）

    A. 2000元B. 2200元C. 2400元D. 2800元

    【答案】B

    【解析】

    设需甲、乙型货车各x、y辆，企业所花的费用为z元，由题意可得关于x，y的不等式组，并得到目标函数，由不等式组作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．

    设需甲、乙型货车各x、y辆，企业所花的费用为z元，

    由题意有，

    由约束条件作出可行域如图：

    化目标函数z=400x+300y为，

    由图可知当x=4,y=2时,z最小值为2200.

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知不等式ax2-5x+b＞0的解是-3＜x＜2，设A={x|bx2-5x+a＞0}，B={x|}．

    （1）求a，b的值；

    （2）求A∩B和A∪（UB）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分10分）选修4—4，坐标系与参数方程

    已知曲线，直线：（为参数）.

    （I）写出曲线的参数方程，直线的普通方程；

    （II）过曲线上任意一点作与夹角为的直线，交于点，的最大值与最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从5本不同的科普书和4本不同的数学书中选出4本，送给4位同学，每人1本，问：

    （1）如果科普书和数学书各选2本，共有多少种不同的送法？（各问用数字作答）

    （2）如果科普书甲和数学书乙必须送出，共有多少种不同的送法？

    （3）如果选出的4本书中至少有3本科普书，共有多少种不同的送法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知斜三棱柱的侧面与底面垂直，，，且，，求：

    （1）侧棱与底面所成角的大小；

    （2）求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知指数函数满足:，定义域为的函数是奇函数.

    (1)求的值；

    (2)判断函数的单调性并用定义加以证明；

    (3)若对任意的 ，不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量， .

    （1）若分别表示将一枚质地均匀的正方体骰子（六个面的点数分别为1,2,3,4,5,6），先后抛掷两次时第一次、第二次出现的点数，求满足的概率；

    （2）若在连续区间上取值，求满足的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

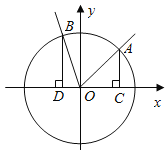
    【题目】（本小题满分13分）如图，在直角坐标系中，角的顶点是原点，始边与轴正半轴重合．终边交单位圆于点，且，将角的终边按逆时针方向旋转，交单位圆于点，记．

    （1）若，求；

    （2）分别过作轴的垂线，垂足依次为，记的面积为，的面积为，若，求角的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数满足①对于任意，都有；②；③的图像与轴的两个交点之间的距离为4.

    （1）求的解析式；

    （2）记

    ①若为单调函数，求的取值范围；

    ②记的最小值为，讨论函数零点的个数.

    查看答案和解析>>

    同步练习册答案