
【题目】已知a∈R,f(x)=aln(x﹣1)+x,f′(2)=2
(1)求a的值,并求曲线y=f(x)在点(2,f(2))处的切线方程y=g(x);
(2)设h(x)=mf′(x)+g(x)+1,若对任意的x∈[2,4],h(x)>0,求实数m的取值范围.
【答案】
(1)解:f(x)=aln(x﹣1)+x,
导数f′(x)= ![]() +1,
+1,
则f′(2)=a+1=2,
解得a=1,f(x)=ln(x﹣1)+1,
f′(x)= ![]() +1,
+1,
可得曲线y=f(x)在点(2,f(2))处的切线斜率为1+1=2,
f(2)=ln1+1=1,
可得曲线y=f(x)在点(2,f(2))处的切线方程为y﹣1=x﹣2,
即为g(x)=x﹣1
(2)解:h(x)=mf′(x)+g(x)+1=m( ![]() +1)+x,
+1)+x,
对任意的x∈[2,4],h(x)>0,
即为m( ![]() +1)+x>0,x∈[2,4],
+1)+x>0,x∈[2,4],
即有m ![]() +x>0,
+x>0,
即为m>(1﹣x)max,x∈[2,4],
由1﹣x≤1﹣2=﹣1,可得m>﹣1.
则实数m的取值范围是(﹣1,+∞)
【解析】(1)求得f(x)的导数,由题意解得a=1,求出曲线y=f(x)在x=2处的切线的斜率和f(2),由点斜式方程可得切线方程;(2)由题意可得m( ![]() +1)+x>0,x∈[2,4],即为m>(1﹣x)max , x∈[2,4],由一次函数的单调性,可得最大值,即可得到m的范围.
+1)+x>0,x∈[2,4],即为m>(1﹣x)max , x∈[2,4],由一次函数的单调性,可得最大值,即可得到m的范围.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4sinxcos(x+ ![]() )+m(x∈R,m为常数),其最大值为2. (Ⅰ)求实数m的值;
)+m(x∈R,m为常数),其最大值为2. (Ⅰ)求实数m的值;
(Ⅱ)若f(α)=﹣ ![]() (﹣
(﹣ ![]() <α<0),求cos2α的值.
<α<0),求cos2α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x(0<x≤10)与销售价格y(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
参考公式: 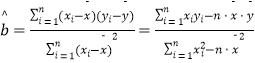 ,
, ![]() .
.
(1)若这两个变量呈线性相关关系,试求y关于x的回归直线方程 ![]() ;
;
(2)已知小王只收购使用年限不超过10年的二手车,且每辆该型号汽车的收购价格为ω=0.03x2﹣1.81x+16.2万元,根据(1)中所求的回归方程,预测x为何值时,小王销售一辆该型号汽车所获得的利润L(x)最大? (销售一辆该型号汽车的利润=销售价格﹣收购价格)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=  ,有下列5个结论: ①任取x1 , x2∈[0,+∞),都有|f(x1)﹣f(x2)|≤2;
,有下列5个结论: ①任取x1 , x2∈[0,+∞),都有|f(x1)﹣f(x2)|≤2;
②函数y=f(x)在区间[4,5]上单调递增;
③f(x)=2kf(x+2k)(k∈N+),对一切x∈[0,+∞)恒成立;
④函数y=f(x)﹣ln(x﹣1)有3个零点;
⑤若关于x的方程f(x)=m(m<0)有且只有两个不同实根x1 , x2 , 则x1+x2=3.
则其中所有正确结论的序号是 . (请写出全部正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别是a,b,c,且A、B、C成等差数列
(1)若 ![]() ,求△ABC的面积
,求△ABC的面积
(2)若sinA、sinB、sinC成等比数列,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+1)x+b.
(1)若f(x)<0的解集为(﹣1,3),求a,b的值;
(2)当a=1时,若对任意x∈R,f(x)≥0恒成立,求实数b的取值范围;
(3)当b=a时,解关于x的不等式f(x)<0(结果用a表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知圆C的方程:x2+y2﹣2x﹣4y+4=0,点P是直线l:x﹣2y﹣2=0上的任意点,过P作圆的两条切线PA,PB,切点为A、B,当∠APB取最大值时.
(Ⅰ)求点P的坐标及过点P的切线方程;
(Ⅱ)在△APB的外接圆上是否存在这样的点Q,使|OQ|= ![]() (O为坐标原点),如果存在,求出Q点的坐标,如果不存在,请说明理由.
(O为坐标原点),如果存在,求出Q点的坐标,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com