
分析 (1)由正弦定理把已知等式化边为角,利用两角和的正弦化简即可求得角B的大小;
(2)由数量积为4可得ac的值,再由余弦定理整体运算求得a+c的值.
解答 解:(1)∵bcosA=(2c-a)cosB,
由正弦定理得sinBcosA=2sinCcosB-sinAcosB,
即sin(A+B)=2sinCcosB=sinC,
∵sinC≠0,∴cosB=$\frac{1}{2}$.
又B∈(0,π),∴B=$\frac{π}{3}$;
(2)∵$\overrightarrow{BA}•\overrightarrow{BC}=4$,∴ca•cosB=4,得ac=8.
由余弦定理得b2=a2+c2-2accosB=a2+c2-ac=(a+c)2-3ac=(a+c)2-24=16.
∴$a+c=2\sqrt{10}$.
点评 本题考查平面向量的数量积运算,考查了正弦定理和余弦定理在解三角形中的应用,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{12}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | [1,2] | C. | [2,4] | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
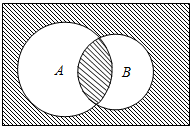
| A. | ∁UA∪(A∩B) | B. | ∁UA∩∁UB | C. | ∁UA∪∁UB | D. | ∁U(A∪B)∪(A∩B) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com