
下列命题中,真命题的有_________(只填写真命题的序号)
①若 则“
则“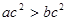 ”是“
”是“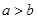 ”成立的充分不必要条件;
”成立的充分不必要条件;
② 当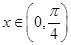 时,函数
时,函数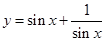 的最小值为2;
的最小值为2;
③ 若命题“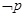 ”与命题“
”与命题“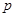 或
或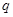 ”都是真命题,则命题
”都是真命题,则命题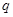 一定是真命题;
一定是真命题;
④ 若命题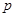 :
: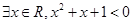 ,则
,则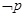 :
: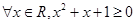 .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
有下列四个命题:
①函数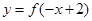 与
与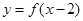 的图象关于
的图象关于 轴对称;②若函数
轴对称;②若函数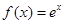 ,则对
,则对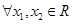 ,都有
,都有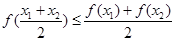 ;③若函数
;③若函数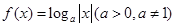 在区间
在区间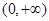 上单调递增,则
上单调递增,则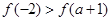 ; ④若函数
; ④若函数 ,则函数
,则函数 的最小值为
的最小值为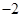 .其中真命题的序号是 .
.其中真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列说法中正确的是 .
①“若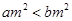 ,则
,则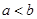 ”的逆命题为真;
”的逆命题为真;
②线性回归方程对应的直线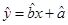 一定经过其样本数据点
一定经过其样本数据点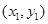 ,
, ,
,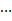 ,
, 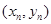 中的一个点;
中的一个点;
③命题“存在实数 ,使得
,使得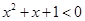 ”的否定是“对任意实数
”的否定是“对任意实数 ,均有
,均有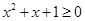 ”
”
④用数学归纳法证明(n+1)(n+2)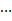 (n+n)=
(n+n)= 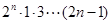 (
(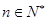 )时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1).
)时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列若干命题中,正确命题的序号是 。
①“a=3”是直线ax+2y+2a=0和直线3x+(a一l)y一a+7 =0平行的充分不必要条件;
②△ABC中,若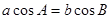 ,则该三角形形状为等腰三角形;
,则该三角形形状为等腰三角形;
③两条异面直线在同一平面内的投影可能是两条互相垂直的直线;
④对于命题 使得
使得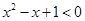 ,则
,则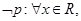 均有
均有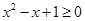 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com