
分析 (1)求出函数的导数,计算f(0),f′(0)的值,求出切线方程即可;
(2)求出f(x)的分段函数的形式,根据a的范围,求出函数的单调区间,从而求出f(x)的最小值即可.
解答 解:(1)a=1,x<1时,f(x)=x3+1-x,
f′(x)=3x2-1,
故f(0)=1,f′(0)=-1,
故切线方程是y=-x+1;
(2)a∈(0,1)时,由已知得f(x)=$\left\{\begin{array}{l}{{x}^{3}+x-a,a≤x≤1}\\{{x}^{3}-x+a,-1≤x<a}\end{array}\right.$,
a<x<1时,由f′(x)>0,得f(x)在(a,1)递增,
-1<x<a时,由f′(x)=3x2-1,
①a∈($\frac{\sqrt{3}}{3}$,1)时,f(x)在(-1,-$\frac{\sqrt{3}}{3}$)递增,在(-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$)递减,在($\frac{\sqrt{3}}{3}$,1)递增,
∴f(x)min=min{f(-1),f($\frac{\sqrt{3}}{3}$)}=min{a,a-$\frac{2\sqrt{3}}{9}$}=a-$\frac{2\sqrt{3}}{9}$,
②a∈(0,$\frac{\sqrt{3}}{3}$]时,f(x)在(-1,-$\frac{\sqrt{3}}{3}$)递增,在(-$\frac{\sqrt{3}}{3}$,a)递减,在(a,1)递增,
∴f(x)min=min{f(-1),f(a)}=min{a,a3}=a3;
综上,f(x)min=$\left\{\begin{array}{l}{a-\frac{2\sqrt{3}}{9},a∈(\frac{\sqrt{3}}{3},1)}\\{{a}^{3},a∈(0,\frac{\sqrt{3}}{3}]}\end{array}\right.$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、考查切线方程问题,是一道中档题.


科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(文)试卷(解析版) 题型:解答题
某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).
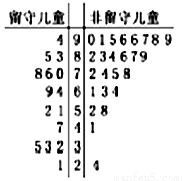
(1)根据茎叶图中的数据完成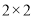 列联表,并判断能否有
列联表,并判断能否有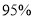 的把握认为孩子的幸福感强与是否是留守儿童有关?
的把握认为孩子的幸福感强与是否是留守儿童有关?
幸福感强 | 幸福感弱 | 总计 | |
留守儿童 | |||
非留守儿童 | |||
总计 |
(2)从15个留守儿童中按幸福感强弱进行分层抽样,共抽取5人,又在这5人中随机抽取2人进行家访,求这2个学生中恰有一人幸福感强的概率.
参考公式: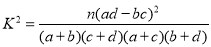
附表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | -3 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
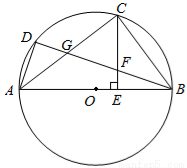
选修4-1:几何证明选讲
如图,已知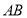 为圆
为圆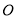 的直径,
的直径,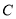 ,
,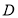 是圆
是圆 上的两个点,
上的两个点,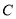 是劣弧
是劣弧 的中点,
的中点,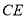 ⊥
⊥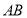 于
于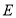 ,
,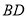 交
交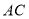 于
于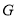 ,交
,交 于
于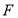 .
.
(1)求证: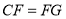 ;
;
(2)求证: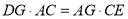 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 非充分非必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com