【题目】在直角坐标系xOy中，圆C：x2+y2+4x﹣2y+m=0与直线x﹣ 
y+ ﹣2=0相切．
（1）求圆C的方程；
（2）若圆C上有两点M，N关于直线x+2y=0对称，且|MN|=2 ，求直线MN的方程．
【答案】
（1）解：圆C：x2+y2+4x﹣2y+m=0，可化为（x+2）2+（y﹣1）2=5﹣m，
∵圆C：x2+y2+4x﹣2y+m=0与直线x﹣ 
y+ ﹣2=0相切，
∴圆心到直线的距离d= 
=2=r，
∴圆C的方程为（x+2）2+（y﹣1）2=4；
（2）解：若圆C上有两点M，N关于直线x+2y=0对称，则设方程为2x﹣y+c=0，
∵|MN|=2 ，
∴圆心到直线的距离d= 
=1，
∴ 
=1，
∴c=5± 
，
∴直线MN的方程为2x﹣y+5± =0．
【解析】（1）利用圆心到直线的距离d=r，求出半径，即可求圆C的方程；（2）若圆C上有两点M，N关于直线x+2y=0对称，则设方程为2x﹣y+c=0，利用|MN|=2 ，可得圆心到直线的距离d= =1，即可求直线MN的方程．
怎样学好牛津英语系列答案科目：高中数学 来源： 题型：
【题目】某市根据地理位置划分成了南北两区，为调查该市的一种经济作物
（下简称
作物）的生长状况，用简单随机抽样方法从该市调查了 500 处 
作物种植点，其生长状况如表：
其中生长指数的含义是：2 代表“生长良好”，1 代表“生长基本良好”，0 代表“不良好，但仍有收成”，﹣1代表“不良好，绝收”．
（1）估计该市空气质量差的
作物种植点中，不绝收的种植点所占的比例；
（2）能否有 99%的把握认为“该市
作物的种植点是否绝收与所在地域有关”？
（3）根据（2）的结论，能否提供更好的调查方法来估计该市
作物的种植点中，绝收种植点的比例？请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱锥P﹣ABC中，PA=PC=5，PB=4，AB=BC=2 
，∠ACB=30°．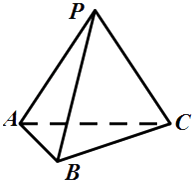 
（1）求证：AC⊥PB；
（2）求三棱锥P﹣ABC的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2﹣2ax+a．
（1）若对任意的实数x都有f（1+x）=f（1﹣x）成立，求实数a的值；
（2）若f（x）在区间[1，+∞）上为单调增函数，求实数a的取值范围；
（3）当x∈[﹣1，1]时，求函数f（x）的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆心在直线y=4x上，且与直线l：x+y﹣2=0相切于点P（1，1）．
（1）求圆的方程；
（2）直线kx﹣y+3=0与该圆相交于A、B两点，若点M在圆上，且有向量 
（O为坐标原点），求实数k．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】等比数列{an}的各项均为正数，且2a1＋3a2＝1， 
＝9a2a6.
(1)求数列{an}的通项公式；
(2)设bn＝log3a1＋log3a2＋…＋log3an，求数列
的前n项和．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
