
 ij�������ȡ������ҵ�������Ͻ�˰���������λ����Ԫ�������������ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�������Ͻ�˰�շ�Χ��[0��100]���������ݷ���Ϊ��һ��[0��20�����ڶ���AA1��ƽ��ABC��������[40��60����������[60��80����������[80��100]��
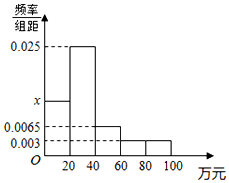
ij�������ȡ������ҵ�������Ͻ�˰���������λ����Ԫ�������������ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�������Ͻ�˰�շ�Χ��[0��100]���������ݷ���Ϊ��һ��[0��20�����ڶ���AA1��ƽ��ABC��������[40��60����������[60��80����������[80��100]������ ��1����Ƶ�ʺ�Ϊ1���з������x��ֵ��
��2�������Ͻ�˰�ղ�����60��Ԫ��Ƶ����Ƶ�����ɣ�
��3�����ݵ�һ����ڶ������ҵ���������ÿ���ȡ�ļ��������оٷ���������¼����������Ӧ�ĸ���ֵ��
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ�ɵã�
20����x+0.025+0.0065+0.003��2��=1��
���x=0.0125��
��2����ҵ�Ͻ�˰�ղ�����60��Ԫ��Ƶ��Ϊ0.003��2��20=0.12��
��1200��0.12=144��
��1200����ҵ����144����ҵ�������������Żݣ�
��3����һ����ڶ������ҵ��֮��Ϊ0.0125��0.025=1��2��
�÷ֲ���������г�ȡ6�ң���һ���ȡ2�ң���ΪA��B��
�ڶ����ȡ4�ң���Ϊc��d��e��f��
����6����ҵ�г�ȡ2�ң������¼�����
AB��Ac��Ad��Ae��Af��Bc��Bd��Be��Bf��cd��ce��cf��de��df��ef��15�֣�
����������ҵ��ͬһ��Ļ����¼�����AB��cd��ce��cf��de��df��ef��7�֣�
������ĸ���ΪP=$\frac{7}{15}$��
���� ������Ҫ������Ƶ�ʷֲ�ֱ��ͼ���оٷ���ŵ���͵ĸ������⣬Ҳ�����˷ֲ����ԭ����Ӧ�����⣬�ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
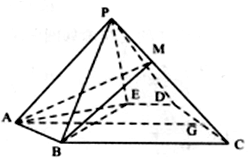 ��ͼ��������P-ABCDE�У���ABE�ǵȱ������Σ��ı���BCDE��ֱ�������ҡ�DEB=��CBE=90�㣬G��CD���е㣬��P�ڵ������Ӱ�����߶�AG�ϣ�
��ͼ��������P-ABCDE�У���ABE�ǵȱ������Σ��ı���BCDE��ֱ�������ҡ�DEB=��CBE=90�㣬G��CD���е㣬��P�ڵ������Ӱ�����߶�AG�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{12}$ | B�� | $\frac{��}{6}$ | C�� | $\frac{��}{4}$ | D�� | $\frac{5��}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16 | B�� | 8 | C�� | 4 | D�� | $2\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com