
分析 根据题目已知中分段函数的解析式$f(x)=\left\{\begin{array}{l}{2^x}+1(0≤x≤1)\\{2^{-x}}+1(-1≤x<0)\end{array}\right.$.然后根据分类标准,设置两个判断框的并设置出判断框中的条件,再由函数各段的解析式,确定判断框的“是”与“否”分支对应的操作,由此即可画出流程图,再编写满足题意的程序
解答 解:(1)将$f(x)=\left\{\begin{array}{l}{2^x}+1(0≤x≤1)\\{2^{-x}}+1(-1≤x<0)\end{array}\right.$
变形为:f(x)=2|x|+1,-1≤x≤1
(2)按原函数设计的程序框图如图②
设计的程序框图如图①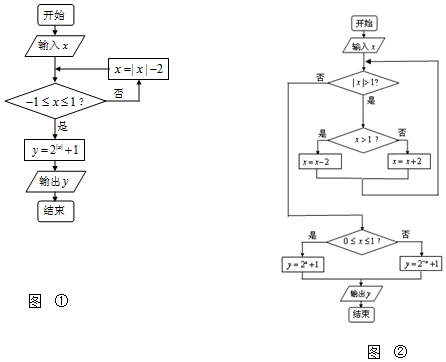
点评 本题考查了设计程序框图解决实际问题.主要考查编写程序解决分段函数问题.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:解答题
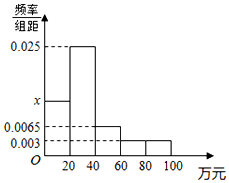 某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为第一组[0,20),第二组AA1⊥平面ABC,第三组[40,60),第四组[60,80),第五组[80,100].
某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为第一组[0,20),第二组AA1⊥平面ABC,第三组[40,60),第四组[60,80),第五组[80,100].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恰为500次 | B. | 恰为600次 | C. | 500次左右 | D. | 600次左右 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男性公务员 | 女性公务员 | 总计 | |
| 有意愿生二胎 | 30 | 15 | 45 |
| 无意愿生二胎 | 20 | 25 | 45 |
| 总计 | 50 | 40 | 90 |
| P(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2$\sqrt{2}$,+∞) | B. | (-2$\sqrt{2}$,2$\sqrt{2}$) | C. | (-2$\sqrt{2}$,1]∪[2$\sqrt{2}$,+∞) | D. | (-∞,2$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | XA+XB=2XM | B. | XA•XB=X${\;}_{M}^{2}$ | C. | $\frac{1}{{X}_{A}}$+$\frac{1}{{X}_{B}}$=$\frac{2}{{X}_{M}}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com