
【题目】已知正方体![]() 棱长为
棱长为![]() ,如图,
,如图,![]() 为
为![]() 上的动点,
上的动点,![]() 平面
平面![]() .下面说法正确的是( )
.下面说法正确的是( )
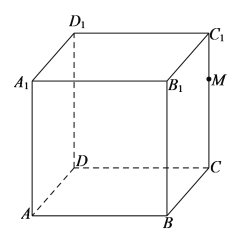
A.直线![]() 与平面
与平面![]() 所成角的正弦值范围为
所成角的正弦值范围为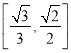
B.点![]() 与点
与点![]() 重合时,平面
重合时,平面![]() 截正方体所得的截面,其面积越大,周长就越大
截正方体所得的截面,其面积越大,周长就越大
C.点![]() 为
为![]() 的中点时,若平面
的中点时,若平面![]() 经过点
经过点![]() ,则平面
,则平面![]() 截正方体所得截面图形是等腰梯形
截正方体所得截面图形是等腰梯形
D.己知![]() 为
为![]() 中点,当
中点,当![]() 的和最小时,
的和最小时,![]() 为
为![]() 的中点
的中点
【答案】AC
【解析】
以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,利用空间向量法可判断A选项的正误;证明出
,利用空间向量法可判断A选项的正误;证明出![]() 平面
平面![]() ,分别取棱
,分别取棱![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的中点
的中点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,比较
,比较![]() 和六边形
和六边形![]() 的周长和面积的大小,可判断B选项的正误;利用空间向量法找出平面
的周长和面积的大小,可判断B选项的正误;利用空间向量法找出平面![]() 与棱
与棱![]() 、
、![]() 的交点
的交点![]() 、
、![]() ,判断四边形
,判断四边形![]() 的形状可判断C选项的正误;将矩形
的形状可判断C选项的正误;将矩形![]() 与矩形
与矩形![]() 延展为一个平面,利用
延展为一个平面,利用![]() 、
、![]() 、
、![]() 三点共线得知
三点共线得知![]() 最短,利用平行线分线段成比例定理求得
最短,利用平行线分线段成比例定理求得![]() ,可判断D选项的正误.
,可判断D选项的正误.
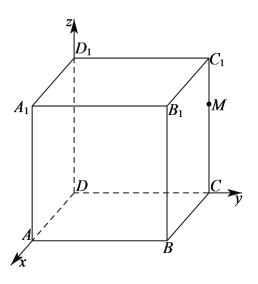
对于A选项,以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,则点
,则点![]() 、
、![]() 、设点
、设点![]() ,
,
![]() 平面
平面![]() ,则
,则![]() 为平面
为平面![]() 的一个法向量,且
的一个法向量,且![]() ,
,![]() ,
,
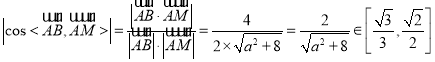 ,
,
所以,直线![]() 与平面
与平面![]() 所成角的正弦值范围为
所成角的正弦值范围为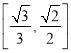 ,A选项正确;
,A选项正确;
对于B选项,当![]() 与
与![]() 重合时,连接
重合时,连接![]() 、
、![]() 、
、![]() 、
、![]() ,
,
在正方体![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是正方形,则
是正方形,则![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,同理可证
,同理可证![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
易知![]() 是边长为
是边长为![]() 的等边三角形,其面积为
的等边三角形,其面积为![]() ,周长为
,周长为![]() .
.
设![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的中点,
的中点,
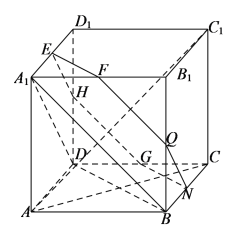
易知六边形![]() 是边长为
是边长为![]() 的正六边形,且平面
的正六边形,且平面![]() 平面
平面![]() ,
,
正六边形![]() 的周长为
的周长为![]() ,面积为
,面积为![]() ,
,
则![]() 的面积小于正六边形
的面积小于正六边形![]() 的面积,它们的周长相等,B选项错误;
的面积,它们的周长相等,B选项错误;
对于C选项,设平面![]() 交棱
交棱![]() 于点
于点![]() ,点
,点![]() ,
,![]() ,
,
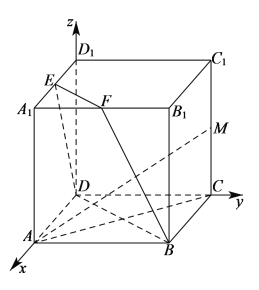
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,即
,即![]() ,得
,得![]() ,
,![]() ,
,
所以,点![]() 为棱
为棱![]() 的中点,同理可知,点
的中点,同理可知,点![]() 为棱
为棱![]() 的中点,则
的中点,则![]() ,
,![]() ,
,
而![]() ,
,![]() ,
,![]() 且
且![]() ,
,
由空间中两点间的距离公式可得![]() ,
,![]() ,
,![]() ,
,
所以,四边形![]() 为等腰梯形,C选项正确;
为等腰梯形,C选项正确;
对于D选项,将矩形![]() 与矩形
与矩形![]() 延展为一个平面,如下图所示:
延展为一个平面,如下图所示:
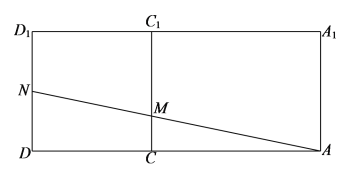
若![]() 最短,则
最短,则![]() 、
、![]() 、
、![]() 三点共线,
三点共线,
![]() ,
,![]() ,
,
![]() ,所以,点
,所以,点![]() 不是棱
不是棱![]() 的中点,D选项错误.
的中点,D选项错误.
故选:AC.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了治疗某种疾病,某科研机构研制了甲、乙两种新药,为此进行白鼠试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药一轮的治疗结果得出后,再安排下一轮试验.4轮试验后,就停止试验.甲、乙两种药的治愈率分别是![]() 和
和![]() .
.
(1)若![]() ,求2轮试验后乙药治愈的白鼠比甲药治愈的白鼠多1只的概率;
,求2轮试验后乙药治愈的白鼠比甲药治愈的白鼠多1只的概率;
(2)已知A公司打算投资甲、乙这两种新药的试验耗材费用,甲药和乙药一次试验耗材花费分别为3千元和![]() 千元,每轮试验若甲、乙两种药都治愈或都没有治愈,则该科研机构和A公司各承担该轮试验耗材总费用的50%;若甲药治愈,乙药未治愈,则A公司承担该轮试验耗材总费用的75%,其余由科研机构承担,若甲药未治愈,乙药治愈,则A公司承担该轮试验耗材总费用的25%,其余由科研机构承担.以A公司每轮支付试验耗材费用的期望为标准,求A公司4轮试验结束后支付试验耗材最少费用为多少元?
千元,每轮试验若甲、乙两种药都治愈或都没有治愈,则该科研机构和A公司各承担该轮试验耗材总费用的50%;若甲药治愈,乙药未治愈,则A公司承担该轮试验耗材总费用的75%,其余由科研机构承担,若甲药未治愈,乙药治愈,则A公司承担该轮试验耗材总费用的25%,其余由科研机构承担.以A公司每轮支付试验耗材费用的期望为标准,求A公司4轮试验结束后支付试验耗材最少费用为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)点![]() 为椭圆
为椭圆![]() 上一动点,连接
上一动点,连接![]() 、
、![]() ,设
,设![]() 的角平分线
的角平分线![]() 交椭圆
交椭圆![]() 的长轴于点
的长轴于点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 只能同时满足下列三个条件中的两个:①函数
只能同时满足下列三个条件中的两个:①函数![]() 的最大值为2;②函数
的最大值为2;②函数![]() 的图象可由
的图象可由![]() 的图象平移得到;③函数
的图象平移得到;③函数![]() 图象的相邻两条对称轴之间的距离为
图象的相邻两条对称轴之间的距离为![]() .
.
(1)请写出这两个条件序号,并求出![]() 的解析式;
的解析式;
(2)求方程![]() 在区间
在区间![]() 上所有解的和.
上所有解的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC的中点.将△ABD沿BD折起,使AB⊥AC,连接AE,AC,DE,得到三棱锥A-BCD.
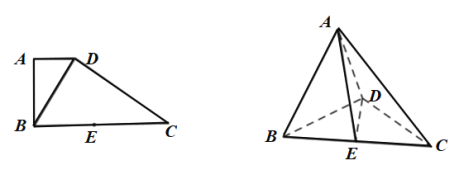
(1)求证:平面ABD⊥平面BCD
(2)若AD=1,二面角C-AB-D的余弦值为![]() ,求二面角B-AD-E的正弦值.
,求二面角B-AD-E的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程是:
的参数方程是: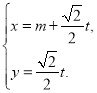 (
(![]() 是参数).以原点
是参数).以原点![]() 为极点,x轴的正半轴为极轴建立极坐标系,曲线
为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,试求实数
,试求实数![]() 值;
值;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,四边形ABCD是边长为2的正方形,△PAD为等边三角形,E,F分别为PC和BD的中点,且EF⊥CD.
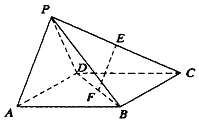
(1)证明:平面PAD⊥平面ABCD;
(2)求点C到平面PDB的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com