练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知Sn为等差数列{an}的前n项和，给出下列两个命题：
    命题p：若S3，S9都大于9，则S6大于11
    命题q：若S6不小于12，则S3，S9中至少有1个不小于9．
    那么，下列命题为真命题的是（　　）
    A．￢pB．（￢p）∧（￢q）C．p∧qD．p∧（￢q）

    分析 由等差数列的前n项和的性质可得：S3，S6-S3，S9-S6成等差数列，即可判断出命题p，q的真假．

    解答 解：对于命题p：由等差数列的前n项和的性质可得：S3，S6-S3，S9-S6成等差数列，∴2（S6-S3）=S3+S9-S6，∴3S6=3S3+S9≥3×9+9，∴S6≥12，因此命题p正确；
    命题q：由上面可知：3S3+S9=3S6≥3×12=36，因此S3，S9中至少有1个不小于9，是真命题．
    那么，下列命题为真命题的是p∧q．
    故选：C．

    点评 本题考查了等差数列的前n项和的性质、复合命题真假的判定方法、不等式的性质，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．在平面直角坐标系xOy中，P为双曲线x2-y2=1右支上一个动点．若点P到直线x-y+2=0的距离大于t恒成立，则实数t的最大值为$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．若△ABC是半径为$\sqrt{5}$的圆O的内接三角形，3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow{0}$，则$\overrightarrow{OC}$•$\overrightarrow{AB}$为（　　）
    A．1B．-1C．6D．-6

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．等比数列{an}中，a3=16，a5=4，则a7=（　　）
    A．1B．-1C．±1D．$\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．实数x，y满足条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{-2x+3y+5≥0}\end{array}\right.$，则目标函数z=x+2y的最大值为（　　）
    A．5B．4C．-1D．$\frac{16}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

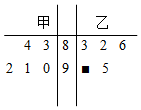    19．如图的茎叶图表示的是甲、乙两人在5天内加工零件的个数，其中一个数字不小心被污损，已知甲的平均数等于乙的平均数，则污损的数字是（　　）
    A．5B．1C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知集合A={x|x2-2x-8＞0}，B={-3，-1，1，3，5}，则A∩B=（　　）
    A．{-1，1，3}B．{-3，-1，1}C．{-3，5}D．{3，5}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若复数z满足（1+2i）•z=|2-i|，则$\overline{z}$（　　）
    A．1+2iB．$\sqrt{5}$（1-2i）C．$\frac{\sqrt{5}}{5}$（1+2i）D．$\frac{\sqrt{5}}{5}$（1-2i）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．下列命题是假命题的是（　　）
    A．?φ∈R，函数f（x）=sin（2x+φ）都不是偶函数
    B．?α，β∈R，使cos（α+β）=cosα+cosβ
    C．向量$\overrightarrow a$=（-2，1），$\overrightarrow b$=（-3，0），则$\overrightarrow a$在$\overrightarrow b$方向上的投影为2
    D．“|x|≤1”是“x＜1”的既不充分也不必要条件

    查看答案和解析>>

    同步练习册答案