
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,四边形
,四边形![]() 是矩形,
是矩形, ![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
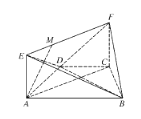
(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)证明线面平行,一般方法为利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找往往利用平几知识,如本题设![]() 与
与![]() 交于点
交于点![]() ,利用三角形相似可得
,利用三角形相似可得![]() ,再根据平行四边形性质可得
,再根据平行四边形性质可得![]() ,(2)求线面角,关键在找平面
,(2)求线面角,关键在找平面![]() 的垂线,由
的垂线,由![]() ,
, ![]() 可得:
可得: ![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,因此过点
,因此过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,则由面面垂直性质定理可得
,则由面面垂直性质定理可得![]() 平面
平面![]() .又
.又![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,最后根据直角三角形求线面角.
的距离,最后根据直角三角形求线面角.
试题解析:(1)证明:在梯形![]() 中,
中,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴四边形![]() 是等腰梯形,且
是等腰梯形,且![]() ,
, ![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() .
.
设![]() 与
与![]() 交于点
交于点![]() ,
, ![]() ,
,
由角平分线定理知: ![]() ,连接
,连接![]() ,
,
则![]() 且
且![]() ,
,
∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)由题知: ![]() ,∴点
,∴点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,过点
的距离,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() .
.
在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,
,
即直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
【题目】.如图,在三棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD,则下列结论中不一定成立的是 ( )
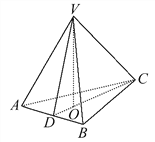
A. AC=BC
B. VC⊥VD
C. AB⊥VC
D. S△VCD·AB=S△ABC·VO
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】16艘轮船的研究中,船的吨位区间为[192,3 246](单位:吨),船员的人数5~32人,船员人数y关于吨位x的回归方程为![]() =9.5+0.006 2x,
=9.5+0.006 2x,
(1)若两艘船的吨位相差1 000,求船员平均相差的人数.
(2)估计吨位最大的船和最小的船的船员人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线C1![]() (t为参数),C2
(t为参数),C2 ![]() (θ为参数),
(θ为参数),
(Ⅰ)当α=![]() 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(Ⅱ)过坐标原点O做C1的垂线,垂足为A,P为OA中点,当α变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)在如图所示的五面体中,面![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是边长为2的正三角形.
是边长为2的正三角形.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某商品在过去的20天内的价格![]() (单位:元)与销售量
(单位:元)与销售量![]() (单位:件)均为时间
(单位:件)均为时间![]() (单位:天)的函数,且价格满足
(单位:天)的函数,且价格满足![]() ,销售量满足
,销售量满足![]() ,其中
,其中![]() ,
, ![]() .
.
(1)请写出该商品的日销售额![]() (单位:元)与时间
(单位:元)与时间![]() (单位:天)的函数解析式;
(单位:天)的函数解析式;
(2)求该商品的日销售额的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点与其短轴得一个端点是正三角形的三个顶点,点
的左右焦点与其短轴得一个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆交于
与椭圆交于![]() 两点,与
两点,与![]() 轴,
轴, ![]() 轴分别相交于点
轴分别相交于点![]() 合点
合点![]() ,且
,且![]() ,点
,点![]() 时点
时点![]() 关于
关于![]() 轴的对称点,
轴的对称点, ![]() 的延长线交椭圆于点
的延长线交椭圆于点![]() ,过点
,过点![]() 分别做
分别做![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .
.
(1) 求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得点
,使得点![]() 平分线段
平分线段![]() ?若存在,请求出直线
?若存在,请求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com