
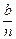 Ԫ��Ȼ���ٽ�������n������2λְ�������˷�����������һ����ÿλְ�����������ʣ�ಿ����Ϊ��˾��չ����.
Ԫ��Ȼ���ٽ�������n������2λְ�������˷�����������һ����ÿλְ�����������ʣ�ಿ����Ϊ��˾��չ����.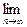 Pn(b).
Pn(b). (1��
(1�� )k��1b; (2) ������䷽�������ˡ����ͷ��䡱���Դ��������ԭ��(3)
)k��1b; (2) ������䷽�������ˡ����ͷ��䡱���Դ��������ԭ��(3) .
. ��
�� (1��
(1�� )b��
)b�� (1��
(1�� )2b������
)2b������ (1��
(1�� )k��1b;
)k��1b; (1��
(1�� )k��1b��0���˽�����䷽�������ˡ����ͷ��䡱���Դ��������ԭ��
)k��1b��0���˽�����䷽�������ˡ����ͷ��䡱���Դ��������ԭ�� )b,f2(b)=(1��
)b,f2(b)=(1�� )2b,��,fk(b)=(1��
)2b,��,fk(b)=(1�� )kb.
)kb. )nb,
)nb, .
.


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
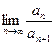 ��
�� )��1.
)��1.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
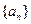 ��ǰ
��ǰ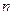 ��Ϊ
��Ϊ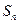 ����֪
����֪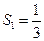 ��
��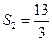 ��
��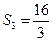 ��
��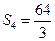 ��
��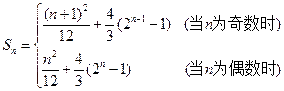 ��
��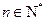 ����
���� 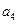 ��������
��������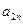 ��������ͣ�
��������ͣ�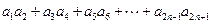 ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
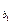 ,a
,a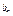 ,��,a
,��,a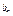 ,��Ϊ�ȱ����У�����b1=1,b2=5,b3=17.
,��Ϊ�ȱ����У�����b1=1,b2=5,b3=17.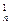 b1+C
b1+C b2+C
b2+C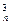 b3+��+C
b3+��+C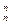 bn,��
bn,��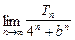 .
.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
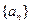 �Ǹ��Ϊ���������У�
�Ǹ��Ϊ���������У�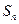 Ϊ��ǰ
Ϊ��ǰ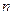 ��ĺͣ���
��ĺͣ���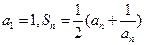
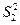 ��
��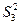 ��ֵ����II��������
��ֵ����II��������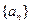 ��ͨ��
��ͨ��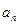 ����III����֤��
����III����֤��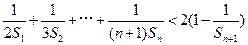
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
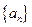 �У���֪
�У���֪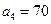 ��
��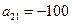 ��
��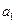 �빫��
�빫��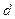 ����д��ͨ�ʽ��
����д��ͨ�ʽ��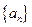 ���ж�������������
���������������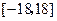 ��
���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com