
【题目】求直线![]() 关于
关于![]() 对称的直线
对称的直线![]() 方程.
方程.
【答案】![]()
【解析】
设![]() 上任意一点
上任意一点![]() 关于
关于![]() 的对称点为
的对称点为![]() 在直线
在直线![]() 上,利用直线
上,利用直线![]() 是
是![]() 的垂直平分线,建立
的垂直平分线,建立![]() 方程关系,将
方程关系,将![]() 用
用![]() 表示,代入直线
表示,代入直线![]() 方程,整理即可;由于
方程,整理即可;由于![]() 相交,可得直线
相交,可得直线![]() 也过该交点,在直线
也过该交点,在直线![]() 再取一点,求出该点关于直线
再取一点,求出该点关于直线![]() 对称点的坐标,且在直线
对称点的坐标,且在直线![]() 上,即可求解;或利用
上,即可求解;或利用![]() 分别与
分别与![]() 夹角相等,设直线
夹角相等,设直线![]() 的斜率为
的斜率为![]() ,确定三直线的方向向量,应用夹角公式建立
,确定三直线的方向向量,应用夹角公式建立![]() 方程,求解即可.
方程,求解即可.
解法1:设![]() 上任意一点
上任意一点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,
则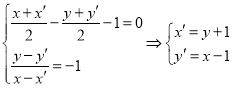 .
.
由于![]() 在直线
在直线![]() 上,
上,
代入得![]() 即
即![]() .
.
解法2:由![]() .故
.故![]() 与
与![]() 交点坐标为
交点坐标为![]() .
.
另取![]() 上不同于
上不同于![]() 的一点
的一点![]() ,设
,设![]() 关于
关于![]() 的对称点
的对称点![]() ,则
,则
 ,即点
,即点![]() 坐标为
坐标为![]() .
.
所以,过![]() 与
与![]() 的直线
的直线![]() 的方程为
的方程为![]() ,
,
即![]() .
.
解法3:由![]() .故
.故![]() 与
与![]() 交点坐标为
交点坐标为![]() .
.
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的一个方向向量为
的一个方向向量为![]() ,
,
又直线![]() 一个方向向量为
一个方向向量为![]() ,直线
,直线![]() 的一个方向向量为
的一个方向向量为![]() ,
,
则![]() (舍),
(舍),![]() .
.
所以,直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】已知某正三棱锥的底面边长为4,侧面与底面所成二面角的余弦值为![]() ,球
,球![]() 为该三棱锥的内切球.球
为该三棱锥的内切球.球![]() 与球
与球![]() 相切,且与该三棱锥的三个侧面也相切,则球
相切,且与该三棱锥的三个侧面也相切,则球![]() 与球
与球![]() 的表面积之比为( )
的表面积之比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为![]() ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为![]() 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与![]() ×S成正比,比例系数为
×S成正比,比例系数为![]() ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为![]() ,记
,记![]() 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=![]() 时。
时。
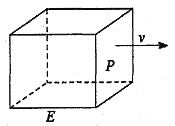
(1)写出![]() 的表达式
的表达式
(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度![]() ,使总淋雨量
,使总淋雨量![]() 最少。
最少。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,泉州市区的房价依旧是市民关心的话题.总体来说,二手房房价有所下降;相比二手房而言,新房市场依然强劲,价格持续升高.已知销售人员主要靠售房提成领取工资.现统计泉州市某新房销售人员2019年一年的工资情况的结果如图所示,则下列说法正确的是( )
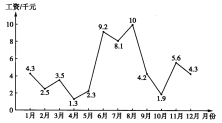
A.2019年该销售人员月工资的中位数为![]()
B.2019年该销售人员8月份的工资增长率最高
C.2019年该销售人员第一季度月工资的方差小于第二季度月工资的方差
D.2019年该销售人员第一季度月工资的平均数大于第四季度月工资的平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体![]() 是正方体,
是正方体,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,点
的中点,点![]() 是棱
是棱![]() 上的动点,过点
上的动点,过点![]() ,
,![]() ,
,![]() 的平面与棱
的平面与棱![]() 交于点
交于点![]() ,则以下说法不正确的是( )
,则以下说法不正确的是( )
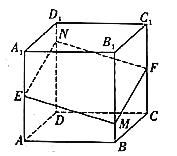
A.四边形![]() 是平行四边形
是平行四边形
B.四边形![]() 是菱形
是菱形
C.当点![]() 从点
从点![]() 往点
往点![]() 运动时,四边形
运动时,四边形![]() 的面积先增大后减小
的面积先增大后减小
D.当点![]() 从点
从点![]() 往点
往点![]() 运动时,三棱锥
运动时,三棱锥![]() 的体积一直增大
的体积一直增大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为原点,抛物线![]() 的准线与y轴的交点为H,P为抛物线C上横坐标为4的点,已知点P到准线的距离为5.
的准线与y轴的交点为H,P为抛物线C上横坐标为4的点,已知点P到准线的距离为5.
(1)求C的方程;
(2)过C的焦点F作直线l与抛物线C交于A,B两点,若以AH为直径的圆过B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,且
,且![]() .过椭圆的右焦点
.过椭圆的右焦点![]() 作长轴的垂线与椭圆,在第一象限交于点
作长轴的垂线与椭圆,在第一象限交于点![]() ,且满足
,且满足![]() .
.
(1)求椭圆的标准方程;
(2)若矩形![]() 的四条边均与椭圆相切,求该矩形面积的取值范围.
的四条边均与椭圆相切,求该矩形面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com