
已知f(x)=ax2(a∈R), g(x)=2lnx.
(1)讨论函数F(x)=f(x)-g(x)的单调性;
(2)是否存在实数 a,使得f(x)≥g(x)+2 (x>0)恒成立,若不存在,请说明理由;若存在,求出a的取值范围;
a,使得f(x)≥g(x)+2 (x>0)恒成立,若不存在,请说明理由;若存在,求出a的取值范围;
(3)若方程f(x)=g(x)在区间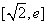 上有两个不相等的实数根,求a的取值范围.
上有两个不相等的实数根,求a的取值范围.
 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
平面 几何中,有边长为
几何中,有边长为 的正三角形内任一点到三边距离之和为定值
的正三角形内任一点到三边距离之和为定值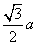 ,类比上述命题,棱长为
,类比上述命题,棱长为 的正四面体内任一点到四个面的距离之和为 ( )
的正四面体内任一点到四个面的距离之和为 ( )
A.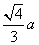 B.
B.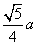 C.
C.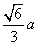 D.
D.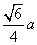
查看答案和解析>>
科目:高中数学 来源: 题型:
某工厂生产甲、乙、丙三种型号的产品,产品数量之比为
3∶5∶7,现用分层抽样的方法抽出容量为n的样本,其中乙种产品有30件,则样本容量n=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
用反证法证明命题:“若整数系数一元二次方程ax2+bx+c=0(a≠o)有有理根,那么 a,b,c中至少有一个是偶数”时,应假设( )
A.a,b,c中至多一个是偶数 B.a,b,c中至少一个是奇数
C.a,b,c中全是奇数 D.a,b,c中恰有一个偶数
查看答案和解析>>
科目:高中数学 来源: 题型:
在斜三棱柱ABC – A1B1Cl中,侧面A1ACC1⊥底面ABC,
A1C= CA= AB=a,AA1=  a,AB⊥AC,D为AA1的中点.
a,AB⊥AC,D为AA1的中点.
(Ⅰ)求证:CD⊥平面ABB1Al
 (Ⅱ)在侧棱BB1上确定一点E,使得二面角E- A1C1一A的大小为
(Ⅱ)在侧棱BB1上确定一点E,使得二面角E- A1C1一A的大小为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com