
| A. | (x,f(-x)) | B. | (x,-f(x)) | C. | (-x,-f(x)) | D. | (-x,f(x)) |
分析 根据条件判断函数的奇偶性即可得到结论.
解答 解:∵f(x)=|$\frac{π}{4}$-sinx|-|$\frac{π}{4}$+sinx|,
∴f(-x)=|$\frac{π}{4}$-sin(-x)|-|$\frac{π}{4}$+sin(-x)|=|$\frac{π}{4}$+sinx|-|$\frac{π}{4}$-sinx|=-(|$\frac{π}{4}$-sinx|-|$\frac{π}{4}$+sinx|)=-f(x),
即函数f(x)是奇函数,
则(-x,-f(x))定在函数y=f(x)图象上,
故选:C
点评 本题主要考查函数奇偶性的性质,利用条件-判断函数的奇偶性是解决本题的关键.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 12 | C. | 24 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1-$\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 办理业务所需的时间Y/分 | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
| A. | 0.22 | B. | 0.24 | C. | 0.30 | D. | 0.31 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
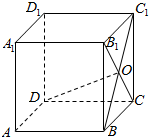 如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.
如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com