
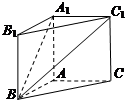
 在直三棱柱(侧棱垂直底面)ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°.
在直三棱柱(侧棱垂直底面)ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°.| 1-AA12 |
| 2 |
| 1+AA12 |
| 2 |
| 2 |
| 1-AA12 |
| 2 |


科目:高中数学 来源: 题型:
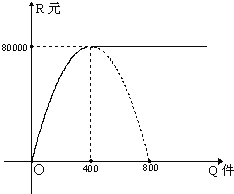 某工厂生产某种产品,固定成本为20000元,每生产一件产品,成本增加100元.已知总收益R是年产量Q(件)的函数,其图象(图中实线部分)如下:当年产量Q在[0,400]内时,为抛物线的一段;当年产量Q>400件时,为一条射线.
某工厂生产某种产品,固定成本为20000元,每生产一件产品,成本增加100元.已知总收益R是年产量Q(件)的函数,其图象(图中实线部分)如下:当年产量Q在[0,400]内时,为抛物线的一段;当年产量Q>400件时,为一条射线.查看答案和解析>>
科目:高中数学 来源: 题型:
| A、实轴在x轴上的双曲线 |
| B、实轴在y轴上的双曲线 |
| C、长轴在x轴上的椭圆 |
| D、长轴在y轴上的椭圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、a⊥α,b?β,a⊥b⇒α⊥β |
| B、α∥β,a⊥α,b∥β⇒a⊥b |
| C、α⊥β,a⊥α,b∥β⇒a⊥b |
| D、α⊥β,α∩β=a,a⊥b⇒b⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x1)f(x2)+1 |
| f(x2)-f(x1) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 天数x | 1 | 2 | 3 | 4 | 5 | 6 |
| 繁殖个数y | 6 | 12 | 25 | 49 | 95 | 190 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com