
| 天数x | 1 | 2 | 3 | 4 | 5 | 6 |
| 繁殖个数y | 6 | 12 | 25 | 49 | 95 | 190 |
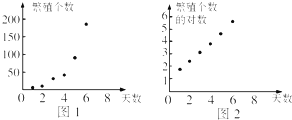
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| z | 1.79 | 2.48 | 3.22 | 3.89 | 4.55 | 5.25 |


科目:高中数学 来源: 题型:
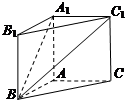 在直三棱柱(侧棱垂直底面)ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°.
在直三棱柱(侧棱垂直底面)ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°.查看答案和解析>>
科目:高中数学 来源: 题型:
| 11π |
| 6 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
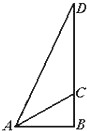 如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30m,在地面上有一点A,测得A、C间的距离为50米,从点A观测电视发射塔的视角为45°(∠CAD=45°),求这座电视发射塔的高度.
如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30m,在地面上有一点A,测得A、C间的距离为50米,从点A观测电视发射塔的视角为45°(∠CAD=45°),求这座电视发射塔的高度.查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com