
过椭圆Γ: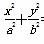 =1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为
=1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为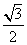 .
.
(1)求椭圆Γ的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆Γ恒有两个交点P,Q,且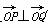 ?若存在,求出该圆的方程;若不存在,请说明理由.
?若存在,求出该圆的方程;若不存在,请说明理由.
解析: (1)由已知得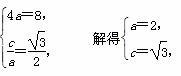 ∴b2=a2-c2=1,
∴b2=a2-c2=1,
故椭圆Γ的方程为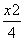 +y2=1.
+y2=1.
(2)假设满足条件的圆存在,其方程为x2+y2=r2(0<r<1).
当直线PQ的斜率存在时,设其方程为y=kx+t,
由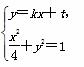 消去y整理得(1+4k2)x2+8ktx+4t2-4=0.
消去y整理得(1+4k2)x2+8ktx+4t2-4=0.
设P(x1,y1),Q(x2,y2),
则x1+x2=-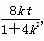 ,x1x2=
,x1x2=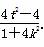 .①
.①
∵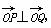 ,∴x1x2+y1y2=0.
,∴x1x2+y1y2=0.
又y1=kx1+t,y2=kx2+t,
∴x1x2+(kx1+t)(kx2+t)=0,
即(1+k2)x1x2+kt(x1+x2)+t2=0.②
将①代入②得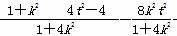 +t2=0,
+t2=0,
即t2=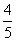 (1+k2).
(1+k2).
∵直线PQ与圆x2+y2=r2相切,
∴r=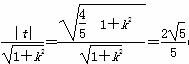 ∈(0,1),
∈(0,1),
∴存在圆x2+y2=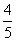 满足条件.
满足条件.
当直线PQ的斜率不存在时,也适合x2+y2=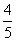 .
.
综上所述,存在圆心在原点的圆x2+y2=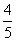 满足条件.
满足条件.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
设函数f(x)=ax+b(0≤x≤1),则a+2b>0是f(x)>0在[0,1]上恒成立的________条件.(填充分但不必要,必要但不充分,充要,既不充分也不必要)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数①f(x)=x2;②f(x)=ex;③f(x)=ln x;④f(x)=cos x.其中对于f(x)定义域内的任意一个x1都存在唯一的x2,使f(x1)f(x2)=1成立的函数是( )
A.① B.②
C.②③ D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=sin +
+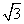 cos ωx(其中ω>0),且函数f(x)的图象的两条相邻的对称轴间的距离为
cos ωx(其中ω>0),且函数f(x)的图象的两条相邻的对称轴间的距离为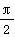 .
.
(1)求ω的值;
(2)将函数y=f(x)的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在区间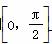 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
若点P(1,1)是圆x2+(y-3)2=9的弦AB的中点,则直线AB的方程为( )
A.x-2y+1=0 B.x+2y-3=0
C.2x+y-3=0 D.2x-y-1=0
查看答案和解析>>
科目:高中数学 来源: 题型:
某农场给某种农作物施肥量x(单位:吨)与其产量y(单位:吨)的统计数据如下表:
| 施肥量x | 2 | 3 | 4 | 5 |
| 产量y | 26 | 39 | 49 | 54 |
根据上表,得到回归直线方程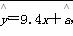 ,当施肥量x=6时,该农作物的预报产量是________.
,当施肥量x=6时,该农作物的预报产量是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,双曲线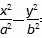 =1(a>0,b>0)的两条渐近线与抛物线y2=4x的准线相交于A,B两点.若△AOB的面积为2,则双曲线的离心率为 .
=1(a>0,b>0)的两条渐近线与抛物线y2=4x的准线相交于A,B两点.若△AOB的面积为2,则双曲线的离心率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com