
| A. | ①② | B. | ②③ | C. | ②④ | D. | ①④ |
分析 ①,若a∥α,b∥α,则a与b位置关系有相交、异面、平行
②,设β为过a的平面,且α∩β=l.由a∥α,得a∥l.由b⊥l,得b⊥a.
③,根据线面垂直的判定定理,可判断;
④,由直线a∥平面α,各平面α中必存在一条直线b与直线a平行,由此根据直线a⊥平面β,利用平面与平面垂直的判定定理得α⊥β.
解答 解:对于①,若a∥α,b∥α,则a与b位置关系有相交、异面、平行,故错;
对于②,设β为过a的平面,且α∩β=l.∵a∥α,∴a∥l.∵直线b⊥平面α,l?α,∴b⊥l,∴b⊥a.故a⊥b.故正确;
对于③,若a?α,b?α,a∥b,c⊥a,c⊥b时,由于a、b不一定相交,故c⊥α不一定成立,故③错误;
对于④,∵直线a∥平面α,∴平面α中必存在一条直线b与直线a平行,∵直线a⊥平面β,∴直线b⊥平面β,∴α⊥β.故正确;
故选:C
点评 本题以命题的真假判断为载体,考查了空间直线和平面的位置关系,熟练掌握空间线面关系的判定定理,性质定理和几何特征是解答的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
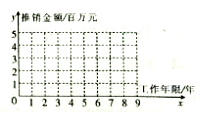 某电脑公司有5名产品推销员,其中工作年限与年推销金额数据如下表:
某电脑公司有5名产品推销员,其中工作年限与年推销金额数据如下表:| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x(年) | 3 | 5 | 6 | 7 | 9 |
| 推销金额y(百万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{{\sqrt{13}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
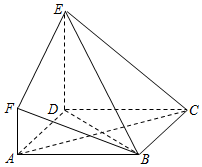 如图所示多面体中,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°
如图所示多面体中,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程x2+ax+b=0至多有一个实根 | B. | 方程x2+ax+b=0至少有一个实根 | ||
| C. | 方程x2+ax+b=0至多有两个实根 | D. | 方程x2+ax+b=0恰好有两个实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 0个或1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-2+\frac{3}{2}i$ | B. | $-2-\frac{3}{2}i$ | C. | $2+\frac{3}{2}i$ | D. | $2-\frac{3}{2}i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com