
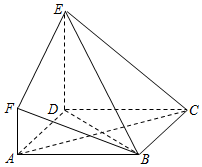
 如图所示多面体中,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°
如图所示多面体中,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°分析 (I)根据∠DBE=60°计算DE,再作出三视图即可;
(II)由DE⊥平面ABCD得出DE⊥AC,结合BD⊥AC得出AC⊥平面BDE;
(III)利用平行线等分线段成比例定理即可得出M为BD的三等分点,再给出证明即可.
解答 解:(Ⅰ)作出三视图如图所示: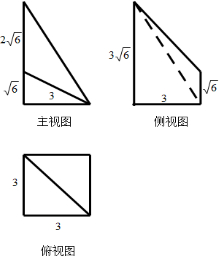
(Ⅱ)证明:因为DE⊥平面ABCD,AC?平面ABCD,
所以DE⊥AC.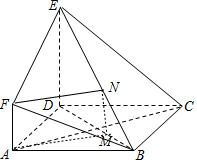
因为底面ABCD是正方形,
所以AC⊥BD,又BD∩DE=D,BD,DE?平面BDE,
∴AC⊥平面BDE.
(Ⅲ)解:在BE上取得N,在BD上取点M,使得$\frac{BM}{BD}=\frac{BN}{BE}=\frac{1}{3}$,
连结MN,FN,AM,
则MN∥DE,$\frac{MN}{DE}$=$\frac{1}{3}$,又AF∥DE,AF=$\frac{1}{3}$DE,
∴AF$\stackrel{∥}{=}$MN,
∴四边形AMNF是平行四边形,
∴AM∥FN,又FN?平面BEF,AM?平面BEF,
∴AM∥平面BEF.
∴当M为BD靠近B的三点分点时,AM∥平面BEF.
点评 本题考查了棱锥的结构特征和三视图,线面垂直、平行的判定,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{e}{4})$ | B. | $(0,\frac{e}{2})$ | C. | (0,1) | D. | (1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com