
分析 (1)利用点的坐标求出向量的坐标,根据向量模的平方等于向量的平方关系得到三角函数的关系,由角的范围求出角的大小.
(2)利用向量垂直的充要条件列出方程,利用三角函数的二倍角公式、切化弦公式化简三角函数,利用三角函数的平方关系求出代数式的值.
解答 解:(1)A(4,0),B(0,4),C(3cosα,3sinα)
∴$\overrightarrow{AC}$=(3cosα-4,3sinα),$\overrightarrow{BC}$=(3cosα,3sinα-4);
又|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,∴${|\overrightarrow{AC}|}^{2}$=${|\overrightarrow{BC}|}^{2}$,
即(3cosα-4)2+9sin2α=9cos2α+(3sinα-4)2,
∴25-24cosα=25-24sinα,
∴sinα=cosα;
又α∈(-π,0),
∴α=-$\frac{3π}{4}$;
(2)∵$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,
∴即(3cosα-4)×3cosα+3sinα×(3sinα-4)=0,
解得sinα+cosα=$\frac{3}{4}$,
所以1+2sinαcosα=$\frac{9}{16}$;
∴2sinαcosα=-$\frac{7}{16}$,
∴$\frac{{2{{sin}^2}α+2sinαcosα}}{1+tanα}$=$\frac{2sinα(sinα+cosα)}{\frac{sinα+cosα}{cosα}}$=2sinαcosα=-$\frac{7}{16}$.
点评 本题考查了平面向量坐标的求法、向量模的坐标公式、由三角函数值求角、三角函数中的二倍角公式、平方关系,是综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 25 | C. | $\sqrt{41}$ | D. | 5$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
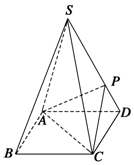 如图,四棱锥S-ABCD的底面是正方形,边长为$\sqrt{2}$,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点.
如图,四棱锥S-ABCD的底面是正方形,边长为$\sqrt{2}$,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
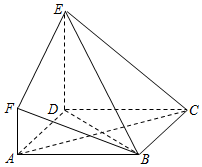 如图所示多面体中,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°
如图所示多面体中,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p:“?x∈R,使得x2+x+1<0”,则¬p:“?x∈R,均有x2+x+1≥0” | |
| B. | “x>1”是“|x|>1”的充分不必要条件 | |
| C. | 若p且q为假命题,则p、q均为假命题 | |
| D. | 命题:“已知f(x)是R上的增函数,若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”的逆否命题为“已知f(x)是R上的增函数,若f(a)+f(b)<f(-a)+f(-b),则a+b<0” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com