
分析 如图建立平面直角坐标系,设A(3a,0),B(0,3b),则三等分点M(a,2b),N(2a,b)
由已知得$\left\{\begin{array}{l}{O{M}^{2}={a}^{2}+4{b}^{2}=si{n}^{2}α}\\{O{N}^{2}=4{a}^{2}+{b}^{2}=co{s}^{2}α}\end{array}\right.$⇒5(a2+b2)=1,则${a}^{2}+{b}^{2}=\frac{1}{5}$,可得AB=$\sqrt{9{a}^{2}+9{b}^{2}}=\frac{3\sqrt{5}}{5}$
解答 解:如图建立平面直角坐标系,设A(3a,0),B(0,3b),
则三等分点M(a,2b),N(2a,b)
由已知得$\left\{\begin{array}{l}{O{M}^{2}={a}^{2}+4{b}^{2}=si{n}^{2}α}\\{O{N}^{2}=4{a}^{2}+{b}^{2}=co{s}^{2}α}\end{array}\right.$⇒
5(a2+b2)=1,则${a}^{2}+{b}^{2}=\frac{1}{5}$
∴AB=$\sqrt{9{a}^{2}+9{b}^{2}}=\frac{3\sqrt{5}}{5}$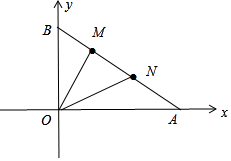
故答案为:$\frac{{3\sqrt{5}}}{5}$.
点评 本题考查了利用坐标处理平面几何问题,转化思想、方程思想是解题的关键,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
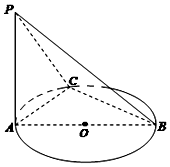 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某电脑公司有5名产品推销员,其中工作年限与年推销金额数据如下表:
某电脑公司有5名产品推销员,其中工作年限与年推销金额数据如下表:| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x(年) | 3 | 5 | 6 | 7 | 9 |
| 推销金额y(百万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 25 | C. | $\sqrt{41}$ | D. | 5$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
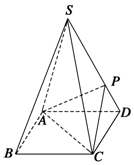 如图,四棱锥S-ABCD的底面是正方形,边长为$\sqrt{2}$,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点.
如图,四棱锥S-ABCD的底面是正方形,边长为$\sqrt{2}$,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
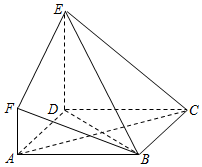 如图所示多面体中,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°
如图所示多面体中,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com