Question

3．对于函数y=f（x），定义域为D=[-2，2]，以下命题正确的是（只要求写出命题的序号）①③④
①若函数y=f（x）在D上具有单调性，且f（0）＞f（1），则y=f（x）是D上的递减函数；
②若f（-1）＜f（0）＜f（1）＜f（2），则y=f（x）是D上的递增函数；
③若f（x）是D上的递减函数，对任意x∈D，使得f（x）-m≥0恒成立，则必须m≤f（2）；
④若f（x）是D上的递增函数，存在x₀∈D，使得f（x₀）-m≥0成立，则必须m≤f（2）．

Answer 1

分析 分别根据函数单调性的定义进行判断和转化即可．

解答 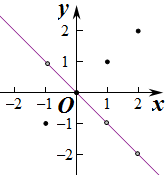解：①若函数y=f（x）在D上具有单调性，且f（0）＞f（1），则y=f（x）是D上的递减函数，正确；
②若f（-1）＜f（0）＜f（1）＜f（2），则y=f（x）是D上的递增函数错误；如图满足条件．，但函数不具备单调性．
③若f（x）是D上的递减函数，则函数的最小值为f（2），对任意x∈D，使得f（x）-m≥0恒成立，则m≤f（x），此时必须m≤f（2）；正确
④若f（x）是D上的递增函数，则f（-2）≤f（x）≤f（2），若存在x₀∈D，使得f（x₀）-m≥0成立，则则m≤f（x），则必须m≤f（2）．正确，
故答案为：①③④．

点评 本题主要考查命题的真假判断，涉及函数单调性的判断和应用，难度不大．