
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
A、y=5sin(3x+
| ||
B、y=5sin(3x-
| ||
| C、y=5sin3x | ||
| D、y=-5sin3x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| an•an+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
sin10°-
|
| 3π |
| 2 |
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
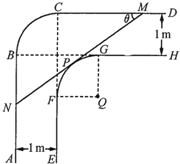 一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD且两组平行墙壁间的走廊宽度都是1m.| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在本市某机关今年的公务员考试成绩中随机抽取25名考生的笔试成绩,并分成5组,得到频率分布直方图如图所示.已知成绩落在第2组[110,120)内的人数为8人.
在本市某机关今年的公务员考试成绩中随机抽取25名考生的笔试成绩,并分成5组,得到频率分布直方图如图所示.已知成绩落在第2组[110,120)内的人数为8人.查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 12 |
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com