
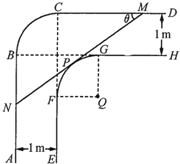
 一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD且两组平行墙壁间的走廊宽度都是1m.| π |
| 4 |
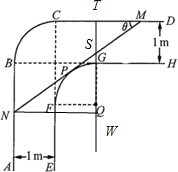 解:(1)如图,设圆弧FG所在的圆的圆心为Q,过Q点作CD的垂线,垂足为点T,且交MN或其延长线于S,并连结PQ,再过点N作TQ的垂线,垂足为W,在Rt△NWS中,因为NW=2,∠SNW=θ,所以NS=
解:(1)如图,设圆弧FG所在的圆的圆心为Q,过Q点作CD的垂线,垂足为点T,且交MN或其延长线于S,并连结PQ,再过点N作TQ的垂线,垂足为W,在Rt△NWS中,因为NW=2,∠SNW=θ,所以NS=| 2 |
| cosθ |
| 1 |
| cosθ |
| 1 |
| cosθ |
| TS |
| sinθ |
| QT-QS |
| sinθ |
| QT-QS |
| sinθ |
| TS |
| sinθ |
| QT-QS |
| sinθ |
| QS-QT |
| sinθ |
| QT-QS |
| sinθ |
| QT-QS |
| sinθ |
| 2 |
| cosθ |
| 2 |
| sinθ |
| 1 |
| sinθcosθ |
| 2sinθ+2cosθ-1 |
| sinθcosθ |
| π |
| 2 |
| π |
| 4 |
2(
| ||||||||
|
| 2 |
| 2 |
| t2-1 |
| 2 |
| 4t-2 |
| t2-1 |
| 2 |
| 4t-2 |
| t2-1 |
| 16m |
| m2+4m-12 |
| 16 | ||
m-
|
| 2 |
| 2 |
| 2 |
| 2 |


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
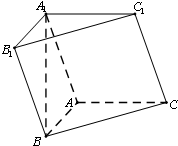 如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.
如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.| 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com