
(本题满分12分)
一列火车在平直的铁轨上行驶,由于遇到紧急情况,火车以速度 (单位:m/s)紧急刹车至停止。求:
(单位:m/s)紧急刹车至停止。求:
(I)从开始紧急刹车到火车完全停止所经过的时间;
(Ⅱ)紧急刹车后火车运行的路程。
(Ⅰ)经过的时间为10s;(Ⅱ)紧急刹车后火车运行的路程为55ln11米。
解析试题分析:(1)求出汽车刹车到停止所需的时间,因为汽车刹车停止后不再运动,然后根据速度时间公式v=v0+at,得到时间。
(2)利用导数的物理意义,可知紧急刹车后火车运行的路程即为 。
。
解:(Ⅰ)令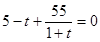 ,注意到t>0,得t=10 (6分)
,注意到t>0,得t=10 (6分)
即经过的时间为10s;
(Ⅱ)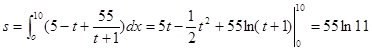
即紧急刹车后火车运行的路程为55ln11米。 (12分)
考点:本题主要考查了物理中汽车刹车停止后不再运动,以及掌握匀变速直线运动的速度时间公式v=v0+at,以及位移的运算。
点评:解决该试题的关键是理解刹车停止的时间,然后利用导数的物理意义得到被积函数速度函数,求解运行的位移即可。


科目:高中数学 来源: 题型:解答题
(本小题满分12分)设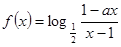 为奇函数,a为常数。
为奇函数,a为常数。
(1)求a的值;
(2)证明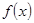 在区间
在区间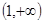 上为增函数;
上为增函数;
(3)若对于区间 上的每一个
上的每一个 的值,不等式
的值,不等式 恒成立,求实数m 的取值范围。
恒成立,求实数m 的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数 ,曲线
,曲线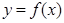 过点
过点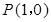 ,且在点
,且在点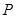 处的切线斜率为2.
处的切线斜率为2.
(Ⅰ)求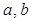 的值;
的值;
(Ⅱ)求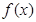 的极值点;
的极值点;
(Ⅲ)对定义域内任意一个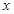 ,不等式
,不等式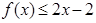 是否恒成立,若成立,请证明;若不成立,请说明理由。
是否恒成立,若成立,请证明;若不成立,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 .
.
(1)讨论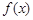 的单调性;
的单调性;
(2)设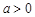 ,证明:当
,证明:当 时,
时,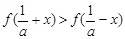 ;
;
(3)若函数 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明: (x0)<0.(本题满分14分)
(x0)<0.(本题满分14分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)已知函数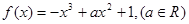
(1)若在 的图象上横坐标为
的图象上横坐标为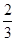 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值;
(2)若 在区间(-2,3)内有两个不同的极值点,求a 取值范围;
在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数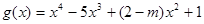 的图象与函数
的图象与函数 的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com