
已知关于 函数
函数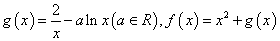 ,
,
(Ⅰ)试求函数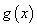 的单调区间;
的单调区间;
(Ⅱ)若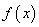 在区间
在区间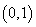 内有极值,试求a的取值范围;
内有极值,试求a的取值范围;
(Ⅲ)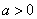 时,若
时,若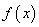 有唯一的零点
有唯一的零点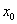 ,试求
,试求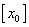 .
.
(注: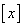 为取整函数,表示不超过
为取整函数,表示不超过 的最大整数,如
的最大整数,如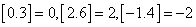 ;以下数据供参考:
;以下数据供参考: )
)
解:(Ⅰ)由题意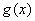 的定义域为
的定义域为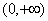
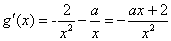
(i)若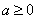 ,则
,则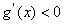 在
在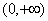 上恒成立,
上恒成立,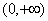 为其单调递减区间;
为其单调递减区间;
(ii)若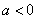 ,则由
,则由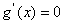 得
得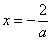 ,
,
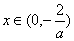 时,
时,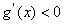 ,
,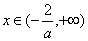 时,
时,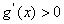 ,
,
所以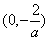 为其单调递减区间;
为其单调递减区间;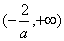 为其单调递增区间;
为其单调递增区间;
(Ⅱ)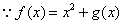
所以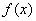 的定义域也为
的定义域也为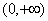 ,且
,且
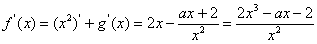
令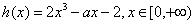 (*)
(*)
则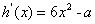 (**)
(**)
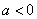 时,
时, 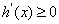 恒成立,所以
恒成立,所以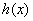 为
为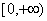 上的单调递增函数,又
上的单调递增函数,又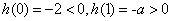 ,所以在区间
,所以在区间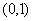 内
内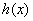 至少存在一个变号零点
至少存在一个变号零点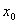 ,且
,且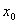 也是
也是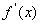 的变号零点,此时
的变号零点,此时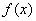 在区间
在区间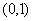 内有极值.
内有极值.
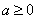 时
时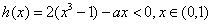 ,即在区间(0,1)上
,即在区间(0,1)上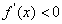 恒成立,此时,
恒成立,此时, 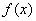 无极值.
无极值.
综上所述,若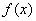 在区间
在区间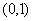 内有极值,则a的取值范围为
内有极值,则a的取值范围为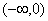 .
.
(Ⅲ)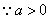 ,由(Ⅱ)且
,由(Ⅱ)且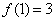 知
知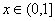 时
时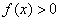 ,
, 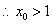 .
.
又由(*)及(**)式知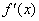 在区间
在区间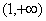 上只有一个极小值点,记为
上只有一个极小值点,记为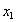 , 且
, 且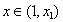 时
时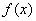 单调递减,
单调递减, 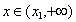 时
时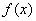 单调递增,由题意
单调递增,由题意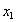 即为
即为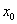 ,
,
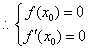
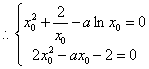
消去a,得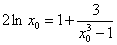
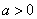 时令
时令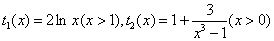 ,
,
则在区间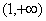 上为
上为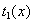 单调递增函数,
单调递增函数, 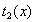 为单调递减函数,
为单调递减函数,
且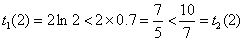
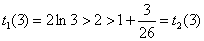
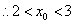
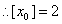


科目:高中数学 来源: 题型:
将一个四棱锥的每个顶点染上一种颜色,并使同一条棱上的两个端点异色,若只有4种颜色可供使用,则不同的染色方法总数有
A.48种 B.72种 C.96种 D.108种
查看答案和解析>>
科目:高中数学 来源: 题型:
在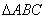 中,边a,b,c的对角分别为A,B,C;且
中,边a,b,c的对角分别为A,B,C;且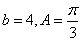 ,面积
,面积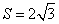 .
.
(Ⅰ)求a的值;
(Ⅱ)设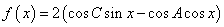 ,将
,将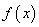 图象上所有点的横坐标变为原来的
图象上所有点的横坐标变为原来的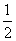 (纵坐标不变)得到
(纵坐标不变)得到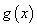 的图象,求
的图象,求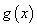 的单调增区间.
的单调增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com