
分析 利用正态分布的意义和3σ原则结合正态分布曲线的对称性,求出概率,即可得出结论.
解答 解:∵一次考试数学成绩X服从N(110,102)正态分布,
∴P(110-2×10<X<110+2×10)=P(90<X<130)=0.954,
∴P(X≥90)=1-$\frac{1-0.954}{2}$=0.977,
∴这个班在这次数学考试中及格(不小于90分)的人数大约是50×0.977≈49.
P(110-1×10<X<110+1×10)=P(100<X<120)=0.683,
∴P(X>120)=$\frac{1}{2}$(1-0.683))=0.1585.
∴这个班在这次数学考试中120分以上的人数大约是50×0.1585≈8.
点评 本题主要考查了连续型随机变量的概率分布正态分布的意义和应用,正态分布曲线的对称性,转化化归的思想方法,属基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
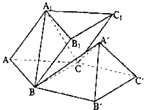 在三棱柱ABC-A1B1C1中,底面ABC为正三角形,AB=A1A=a,BA1=AC,A1C⊥AB.
在三棱柱ABC-A1B1C1中,底面ABC为正三角形,AB=A1A=a,BA1=AC,A1C⊥AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| ξ | 1 | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | $\frac{2}{5}$ | m | $\frac{1}{10}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com