
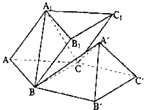
 在三棱柱ABC-A1B1C1中,底面ABC为正三角形,AB=A1A=a,BA1=AC,A1C⊥AB.
在三棱柱ABC-A1B1C1中,底面ABC为正三角形,AB=A1A=a,BA1=AC,A1C⊥AB.分析 (I)过A1作A1H⊥底面ABC,H为垂足,连接CH、BH、AH,推导出H为△ABC的垂心,由此能证明AA1⊥BC.(II)由题知所求旋转过的角就是二面角B1-BC-B′,推导出$∠{B}_{1}B{B}^{'}$为二面角${B}_{1}-BC-{B}^{'}$的平面角,$∠{B}_{1}B{B}^{'}$=∠A1AH,由此能求出所求旋转过的角的余弦值.
解答 证明:(I)过A1作A1H⊥底面ABC,H为垂足,连接CH、BH、AH,
A1B⊥AC,A1H⊥AC,A1B与A1H相交,
∴AC⊥面A1BH,…(2分)
又BH在面A1BH内,∴BH⊥AC,…(3分)
同理CH⊥AB,∴H为△ABC的垂心…(4分)
∴AH⊥BC,又A1H⊥BC,AH与A1H相交,
∴BC⊥面A1AH.又A1A在面A1AH内,
∴AA1⊥BC.…(6分)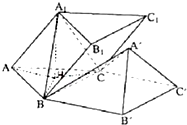 解:(II)由题知所求旋转过的角就是二面角B1-BC-B′,…(7分)
解:(II)由题知所求旋转过的角就是二面角B1-BC-B′,…(7分)
∵AA1∥BB1,由(I)知BB1⊥BC,从而BB′⊥BC,
∴$∠{B}_{1}B{B}^{'}$为二面角${B}_{1}-BC-{B}^{'}$的平面角…(8分)
又BB′∥AH(在底面内AH,BB′同时垂直于BC),
∴$∠{B}_{1}B{B}^{'}$=∠A1AH($∠{B}_{1}B{B}^{'}$和∠A1AH的两边分别平行,且方向相同).…(9分)
∵AB=AA1=a,又H为△ABC的垂心,△ABC为正三角形,
∴H为△ABC的中心,在Rt△A1AH中,
cos∠A1AH=$\frac{AH}{A{A}_{1}}$=$\frac{\frac{2}{3}×(\frac{\sqrt{3}}{2}a)}{a}$=$\frac{\sqrt{3}}{3}$,
∴cos$∠{B}_{1}B{B}^{'}$=$\frac{\sqrt{3}}{3}$.…(11分)
即所求旋转过的角的余弦值为$\frac{\sqrt{3}}{3}$.…(12分
点评 本题考查异面直线垂直的证明,考查角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为k(k>0)的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方).
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为k(k>0)的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
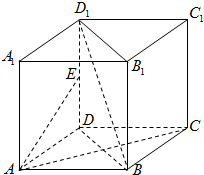 在正方体ABCD-A1B1C1D1中,已知E为DD1的中点.
在正方体ABCD-A1B1C1D1中,已知E为DD1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com