
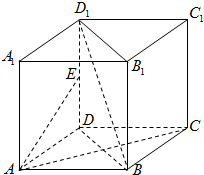
 在正方体ABCD-A1B1C1D1中,已知E为DD1的中点.
在正方体ABCD-A1B1C1D1中,已知E为DD1的中点.分析 (1)证明一条直线垂直一个平面,只需要证明这条直线垂直平面内的两条相交直线即可.
(2)求异面直线所成的角的值,首先通过平移相交,证明异面直线的角,再进行计算.
解答  解:(1)证明:在正方体ABCD-A1B1C1D1中,
解:(1)证明:在正方体ABCD-A1B1C1D1中,
BB1⊥平面ABCD,AC?平面ABCD,所以AC⊥BB1
又∵AC⊥BD,BD,BB1?平面BB1D1D,BD∩BB1,
所以AC⊥平面BB1D1D;
(2)由题意,设AC∩BD=O,连结OE,则O、E分别是BD、DD1的中点,所以OE∥BD1,所以∠OEA=θ就是直线BD1与AE所成的角.
由(1)知,AC⊥平面BB1D1D,又OE?平面BB1D1D,所以AC⊥OE.
设正方体ABCD-A1B1C1D1的棱长为2a,
则$AO=\frac{1}{2}AC=\sqrt{2}a$,$AE=\sqrt{A{D^2}+D{E^2}}=\sqrt{4{a^2}+{a^2}}=\sqrt{5}a$,
在Rt△AOE中,$sinθ=\frac{AO}{AE}=\frac{{\sqrt{2}a}}{{\sqrt{5}a}}=\frac{{\sqrt{10}}}{5}$,
所以:直线BD1与AE所成角的正弦值为$\frac{{\sqrt{10}}}{5}$.
点评 本题考查了线面垂直的证明方法以及异面直线所成角的计算.属于基础题.


科目:高中数学 来源: 题型:解答题
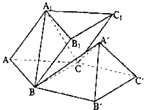 在三棱柱ABC-A1B1C1中,底面ABC为正三角形,AB=A1A=a,BA1=AC,A1C⊥AB.
在三棱柱ABC-A1B1C1中,底面ABC为正三角形,AB=A1A=a,BA1=AC,A1C⊥AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
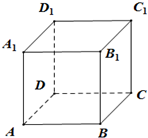 如图,从正方体ABCD-A1B1C1D1的8个顶点中选出的4个点恰为一个正四面体的顶点.
如图,从正方体ABCD-A1B1C1D1的8个顶点中选出的4个点恰为一个正四面体的顶点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com