
分析 先求出f(x)+f(-x)=2,由此能求出f(-$\frac{1}{3}$)+f(-$\frac{1}{2}$)+f(-1)+f(0)+f(1)+f($\frac{1}{2}$)+f($\frac{1}{3}$)的值.
解答 解:∵函数f(x)=$\frac{{2}^{x+1}}{{2}^{x}+1}$,
∴f(x)+f(-x)=$\frac{{2}^{x+1}}{{2}^{x}+1}$+$\frac{{2}^{-x+1}}{{2}^{-x}+1}$=$\frac{{2}^{x+1}}{{2}^{x}+1}$+$\frac{{2}^{\;}}{{2}^{x}+1}$=2,
∴f(-$\frac{1}{3}$)+f(-$\frac{1}{2}$)+f(-1)+f(0)+f(1)+f($\frac{1}{2}$)+f($\frac{1}{3}$)
=2×3+$\frac{2}{{2}^{0}+1}$=7.
故答案为:7.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


科目:高中数学 来源: 题型:解答题
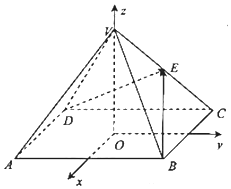 如图,以正四棱锥V-ABCD的底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC中点,正四棱锥的底面边长为2a,高为h,且有cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=-$\frac{15}{49}$.
如图,以正四棱锥V-ABCD的底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC中点,正四棱锥的底面边长为2a,高为h,且有cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=-$\frac{15}{49}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1125$\sqrt{2}$π | B. | 3375$\sqrt{2}$π | C. | 450π | D. | 900π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1-e | B. | e-1 | C. | 1-e | D. | e+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{9}{4}$] | B. | [9,+∞) | C. | (1,$\frac{9}{4}$]∪[9,+∞) | D. | [$\frac{3}{2}$,$\frac{9}{4}$]∪[9,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{y^2}{4}-{x^2}=1$ | C. | ${y^2}-\frac{x^2}{4}=1$ | D. | $\frac{y^2}{16}-\frac{x^2}{4}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com