
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{y^2}{4}-{x^2}=1$ | C. | ${y^2}-\frac{x^2}{4}=1$ | D. | $\frac{y^2}{16}-\frac{x^2}{4}=1$ |
分析 设双曲线的焦点为(0,c),渐近线方程为ax-by=0,由直线和圆相切的条件,求得b=2,再求a,即可得到双曲线C的方程.
解答 解:设双曲线的焦点为(0,c),渐近线方程为ax-by=0,
由于圆与双曲线的渐近线相切,
则$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=2,
化简得,b=2,
因为$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$,即:$\frac{{a}^{2}+{b}^{2}}{{a}^{2}}=\frac{5}{4}$,所以a=2,
所以双曲线的方程为:$\frac{y^2}{16}-\frac{x^2}{4}=1$.
故选:D.
点评 本题考查双曲线的性质,考查直线和圆相切的条件,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
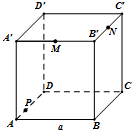 如图,在棱长为a的正方体ABCD-A′B′C′D′中,M、N分别是棱A′B′、B′C′的中点,P是棱AD上一点,AP=$\frac{a}{3}$,过P、M、N的平面与棱CD交于Q,则PQ的长度为$\frac{2\sqrt{\sqrt{2}}}{3}$a.
如图,在棱长为a的正方体ABCD-A′B′C′D′中,M、N分别是棱A′B′、B′C′的中点,P是棱AD上一点,AP=$\frac{a}{3}$,过P、M、N的平面与棱CD交于Q,则PQ的长度为$\frac{2\sqrt{\sqrt{2}}}{3}$a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
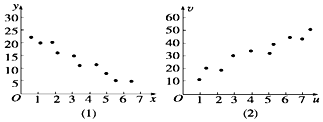 对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);对变量u,v,有观测数据(ui,vi)(i=1,2,…,10),得散点图(2),由这两个散点图可以判断( )
对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);对变量u,v,有观测数据(ui,vi)(i=1,2,…,10),得散点图(2),由这两个散点图可以判断( )| A. | 变量x与y正相关,u与v正相关 | B. | 变量x与y正相关,u与v负相关 | ||
| C. | 变量x与y负相关,u与v正相关 | D. | 变量x与y负相关,u与v负相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
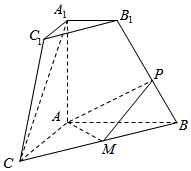 如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2,直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.点M为线段BC的中点,点P是线段BB1中点.
如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2,直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.点M为线段BC的中点,点P是线段BB1中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -2 | C. | 2 | D. | 14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com