
已知正△ABC的边长为 , CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
, CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
(1)试判断折叠后直线AB与平面DEF的位置关系,并说明理由;
(2)若棱锥E-DFC的体积为 ,求
,求 的值;
的值;
(3)在线段AC上是否存在一点P,使BP⊥DF?如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.

(1)平行; (2)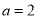 ; (3)存在AP:AC=1:3
; (3)存在AP:AC=1:3
【解析】
试题分析:(1)由于E、F分别是AC和BC边的中点,所以在翻折后的三角形ABC中, .由线面平行的判定定理可得结论.
.由线面平行的判定定理可得结论.
(2)由棱锥E-DFC的体积为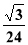 ,因为△ABC沿CD翻折成直二面角A-DC-B,并且
,因为△ABC沿CD翻折成直二面角A-DC-B,并且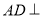 平面BCD,即由三棱锥的体积公式,即可求出结论.
平面BCD,即由三棱锥的体积公式,即可求出结论.
(3)在线段AC上是否存在一点P,使BP⊥DF,即转化为直线与平面垂直的问题,假设存在点P作 ,k为垂足,连结BK即可得到直线DF
,k为垂足,连结BK即可得到直线DF  平面BPK,所以可得
平面BPK,所以可得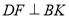 .通过三角形的相似即可得到所求的结论.
.通过三角形的相似即可得到所求的结论.
(1)AB//平面DEF,
如图.在△ABC中,∵E,F分别是AC,BC的中点,故EF//AB,
又AB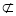 平面DEF,∴AB//平面DEF, 4分
平面DEF,∴AB//平面DEF, 4分
(2)∵AD⊥CD,BD⊥CD, 将△ABC沿CD翻折成直二面角A-DC-B
∴AD⊥BD,AD⊥平面BCD,取CD中点M,则EM//AD,∴EM⊥平面BCD,且EM=a/2
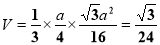 ,a=2. 8分
,a=2. 8分
(3)存在满足条件的点P.
做法:因为三角形BDF为正三角形,过B做BK⊥DF,延长BK交DC于K,过K做KP//DA,交AC于P.则点P即为所求.
证明:∵AD⊥平面BCD , KP//DA,∴PK⊥平面BCD,PK⊥DF,又 BK⊥DF,PK∩BK=K,∴DF⊥平面PKB,DF⊥PB.又∠DBK=∠KBC=∠BCK=30°,∴DK=KF=KC/2.
故AP:OC=1:2,AP:AC=1:3 12分
考点:1.图形的翻折.2.线面间的位置关系.3.开放性题的等价变换.4.空间想象力.


科目:高中数学 来源:2013-2014学年福建省龙岩市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
已知命题p:
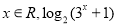 ≤0,则( )
≤0,则( )
A. p是假命题;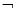 p:
p: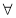
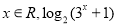 ≤0
≤0
B. p是假命题;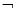 p:
p: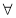
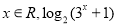 >0
>0
C. p是真命题;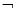 p:
p: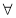
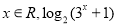 ≤0
≤0
D. p是真命题; p:
p:
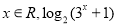 >0
>0
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴文科数学试卷(解析版) 题型:选择题
已知命题 :?
:? ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )
A. :?
:? ,
, ,且
,且 为假命题
为假命题
B. :?
:? ,
, ,且
,且 为真命题
为真命题
C. :?
:? ,
, ,且
,且 为假命题
为假命题
D. :?
:? ,
, ,且
,且 为真命题
为真命题
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习理科数学试卷(解析版) 题型:选择题
在密码理论中,“一次一密”的密码体系是理论上安全性最高的.某部队执行特殊任务使用四个不同的口令 ,每次只能使用其中的一种,且每次都是从上次未使用的三个口令中等可能地随机选用一种.设第1次使用
,每次只能使用其中的一种,且每次都是从上次未使用的三个口令中等可能地随机选用一种.设第1次使用 口令,那么第5次也使用
口令,那么第5次也使用 口令的概率是( )
口令的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习文科数学试卷(解析版) 题型:选择题
如图,半径为R的圆C中,已知弦AB的长为5,则 =( )
=( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高考考前模拟理科数学试卷(解析版) 题型:填空题
若一个四棱锥的三视图如图所示,其中正视图与侧视图都是边长为2的等边三角形,则该四棱锥的四条侧棱长之和等于_____________

查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省漳州市毕业班质量检查理科数学试卷(解析版) 题型:选择题
已 知F1 ,F2分别是双曲线 的左、右焦点,过F1的直线
的左、右焦点,过F1的直线 与双曲线的左、右两支分别
与双曲线的左、右两支分别
交于A、B两点.若ΔABF2是等边三角形,则该双曲线的离心率为
A.2 B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com