
【题目】不等式2x2﹣2axy+y2≥0对任意x∈[1,2]及任意y∈[1,4]恒成立,则实数a取值范围是 .
科目:高中数学 来源: 题型:
【题目】共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是共享经济的一种新形态.一个共享单车企业在某个城市就“一天中一辆单车的平均成本(单位:元)与租用单车的数量(单位:千辆)之间的关系”进行调查研究,在调查过程中进行了统计,得出相关数据见下表:
租用单车数量 | 2 | 3 | 4 | 5 | 8 |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注: ![]() ,
,![]() 称为相应于点
称为相应于点![]() 的残差(也叫随机误差));
的残差(也叫随机误差));
租用单车数量 | 2 | 3 | 4 | 5 | 8 | |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 | -0.1 | 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放.根据市场调查,这个城市投放8千辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.6,0.4;投放1万辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.4,0.6.问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入-成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
直角坐标系![]() 中,直线
中,直线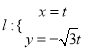 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() .
.
(1)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 交曲线
交曲线![]() 于
于![]() 两点,直线
两点,直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面四边形![]() 中,
中, ![]() ,
, ![]() 为等边三角形,现将
为等边三角形,现将![]() 沿
沿![]() 翻折得到四面体
翻折得到四面体![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.


(Ⅰ)求证:四边形![]() 为矩形;
为矩形;
(Ⅱ)当平面![]() 平面
平面![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|mx|﹣|x﹣n|(0<n<1+m),若关于x的不等式f(x)<0的解集中的整数恰有3个,则实数m的取值范围为( )
A.3<m<6
B.1<m<3
C.0<m<1
D.﹣1<m<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中, 已知定圆
中, 已知定圆![]() ,动圆
,动圆![]() 过点
过点![]() 且与圆
且与圆![]() 相切,记动圆圆心
相切,记动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设![]() 是曲线
是曲线![]() 上两点,点
上两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (异于点
(异于点![]() ),若直线
),若直线![]() 分别交
分别交![]() 轴于点
轴于点![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区一住户在楼顶违规私自建了“阳光房”,该小区其他居民对此意见很大,通过物业和城管部门多次上门协调,该住户终于拆除了“阳光房”,对此有人认为既然已经建成再拆除太可惜了,为此业主委员会通过随机询问小区100名性别不同的居民对此件事情的看法,得到如下的2×2列联表
认为应该拆除 | 认为太可惜了 | 总计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
总计 | 75 | 25 | 100 |
附:
P(K2≥k) | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 5.024 |
K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参照附表,由此可知下列选项正确的是( )
A.在犯错误的概率不超过1%的前提下,认为“是否认为拆除太可惜了与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“是否认为拆除太可惜了与性别无关”
C.有90%以上的把握认为“是否认为拆除太可惜了与性别有关”
D.有90%以上的把握认为“是否认为拆除太可惜了与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇,网购成了大众购物的一个重要组成部分,可人们在开心购物的同时,假冒伪劣产品也在各大购物网站频频出现,为了让顾客能够在网上买到货真价实的好东西,各大购物平台也推出了对商品和服务的评价体系,现从某购物网站的评价系统中选出100次成功的交易,并对其评价进行统计,对商品的好评率为 ![]() ,对服务的好评率为
,对服务的好评率为 ![]() ,其中对商品和服务都做出好评的交易为30次.
,其中对商品和服务都做出好评的交易为30次.
(1)列出关于商品和服务评价的2×2列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为商品好评与服务好评有关?
(2)若针对商品的好评率,采用分层抽样的方式从这100次交易中取出5次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com