练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，某花木场有一块等腰梯形ABCD的空地，其各边中点分别是E、F、G、H，测得对角线BD=12米，现想用篱笆围成四边形EFGH的场地，则需用的篱笆总长度是（ ）

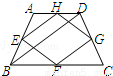
    A.12米 B.24米 C.36米 D.48米

     

    B

    【解析】

    试题分析：根据三角形中位线定理和等腰梯形的对角线相等可证明篱笆的形状为菱形，且边长等于等腰梯形的对角线的一半，即可求得篱笆总长度．

    【解析】
    连接BD．

    根据三角形中位线定理，得

    EF=HG=AC=6，EH=FG=BD．

    ∵四边形ABCD是等腰梯形，

    ∴AC=BD．

    ∴EF=FG=GH=HE=6．

    ∴需篱笆总长度是EF+HG+EH+GF=2BD=2×12=24（米）．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年人教B版选修2-1 第二章 圆锥曲线与方程练习卷（解析版） 题型：填空题

    （5分）（2009•聊城一模）已知抛物线y2=2px（p＞0），过点M（2p，0）的直线与抛物线相交于A，B，= ．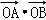

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修四4-1第一讲1.2练习卷（解析版） 题型：选择题

    如图，在△ABC中，M是AC的中点，点E在AB上，且AE=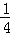AB，连接EM并延长交BC的延长线于点D，则BC：CD=（ ）

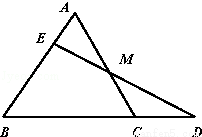
    A.2：1 B.3：1 C.3：2 D.4：1

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修四4-1第一讲1.1练习卷（解析版） 题型：填空题

    将边长为2，一个内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD，点E，F分别为AC，BD的中点，则下列命题中正确的是 ．

    ①EF∥AB；

    ②EF⊥BD；

    ③EF有最大值，无最小值；

    ④当四面体ABCD的体积最大时，；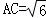

    ⑤AC垂直于截面BDE．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修四4-1第一讲1.1练习卷（解析版） 题型：选择题

    已知，如图，在梯形ABCD中，AD∥BC，AD=3，BC=7，点M，N分别是对角线BD，AC的中点，则MN=（ ）

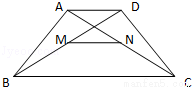
    A.2 B.5 C.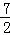 D.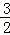

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修一1-2第四章4.2练习卷（解析版） 题型：选择题

    如图所示的框图中“幂函数的定义”“幂函数的图象与性质”与“幂函数”的关系是（ ）

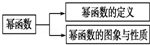
    A.并列关系 B.从属关系 C.包含关系 D.交叉关系

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修一1-2第四章4.2练习卷（解析版） 题型：选择题

    如图是“集合”的知识结构图，如果要加入“子集”，则应该放在（ ）

    A.“集合的概念”的下位 B.“集合的表示”的下位

    C.“基本关系”的下位 D.“基本运算”的下位

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修一1-2第一章1.2练习卷（解析版） 题型：选择题

    （2012•潍坊二模）为了普及环保知识，增强环保意识，某大学从理工类专业的A班和文史类专业的B班各抽取20名同学参加环保知识测试．统计得到成绩与专业的列联表：

     

    优秀

    非优秀

    总计

    A班

    14

    6

    20

    B班

    7

    13

    20

    C班

    21

    19

    40

    附：参考公式及数据：

    （1）卡方统计量（其中n=n11+n12+n21+n22）；

    （2）独立性检验的临界值表：

    P（x2≥k0）

    0.050

    0.010

    K0

    3.841

    6.635

    则下列说法正确的是（ ）

    A.有99%的把握认为环保知识测试成绩与专业有关

    B.有99%的把握认为环保知识测试成绩与专业无关

    C.有95%的把握认为环保知识测试成绩与专业有关

    D.有95%的把握认为环保知识测试成绩与专业无关

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷（解析版） 题型：填空题

    （5分）若方程﹣=1表示双曲线，则k的取值范围是 ．

     

    查看答案和解析>>

    同步练习册答案