
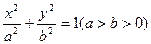
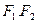
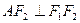
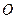
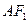
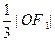
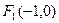 设过点
设过点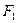 且不与坐标轴垂直的直线交椭圆于
且不与坐标轴垂直的直线交椭圆于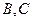 两点,线段
两点,线段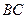 的垂直平分线与x轴交于
的垂直平分线与x轴交于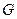 ,求点
,求点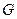 横坐标的取值范围.
横坐标的取值范围.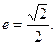 (2)
(2)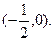
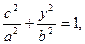
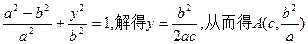 .……………………2分
.……………………2分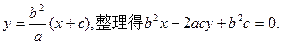
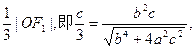 …………4分
…………4分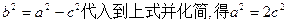 ,进而求得
,进而求得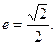 ……6分
……6分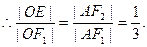 (*)……………………2分
(*)……………………2分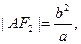 ………………3分
………………3分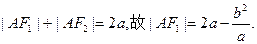 …………4分
…………4分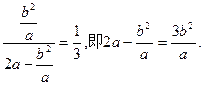
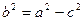 代入并化简,得
代入并化简,得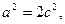 进而求得
进而求得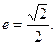 …………6分
…………6分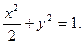 ……………… 7分
……………… 7分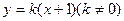 代入椭圆方程并整理得
代入椭圆方程并整理得
|
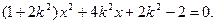
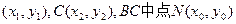
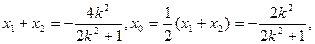
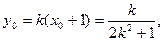 …………………10分
…………………10分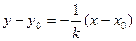 …………… 11分
…………… 11分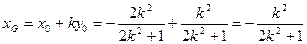
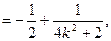 …………12分
…………12分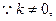
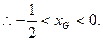 ……………13分
……………13分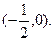 ……………14分
……………14分

科目:高中数学 来源:不详 题型:解答题
 ,
,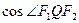 的取值范围;
的取值范围; ,试求直线PM的斜率
,试求直线PM的斜率 的范围。
的范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
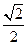 ,且椭圆经过圆C:
,且椭圆经过圆C: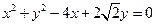 的圆心C。
的圆心C。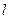 过椭圆的焦点且与圆C相切,求直线
过椭圆的焦点且与圆C相切,求直线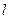 的方程。
的方程。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com