
如图, 是圆
是圆 内两弦
内两弦 和
和 的交点,过
的交点,过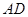 延长线上一点
延长线上一点 作圆
作圆 的切线
的切线 ,
, 为切点,已知
为切点,已知 .求证:
.求证:
(Ⅰ) ∽
∽ ;
;
(Ⅱ) ∥
∥ .
.
(Ⅰ)见解析(Ⅱ)见解析
解析试题分析(Ⅰ)由切割线定理得FG2=FA·FD.由已知EF=FG,由等量代换得EF2=FA·FD,化为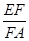 =
=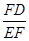 ,因为∠EFA=∠DFE,由相似三角形的判定定理得△FED∽△EAF;
,因为∠EFA=∠DFE,由相似三角形的判定定理得△FED∽△EAF;
(Ⅱ)由(Ⅰ)△FED∽△EAF,由相似三角形性质知,∠FED=∠FAE,由同弧所对的圆周角相等知,∠FAE=∠DAB=∠DCB,由等量代换得,∠FED=∠BCD,由同位角相等两直线平行得EF∥CB,即证出所证结论.
试题解析:(Ⅰ)由切割线定理得FG2=FA·FD.
又EF=FG,所以EF2=FA·FD,即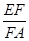 =
=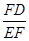 .
.
因为∠EFA=∠DFE,所以△FED∽△EAF. 5分
(Ⅱ)由(Ⅰ)得∠FED=∠FAE.
因为∠FAE=∠DAB=∠DCB,
所以∠FED=∠BCD,所以EF∥CB. 10分
考点:切割线定理,相似三角形判定与性质,圆周角定理,两直线平行的判定


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:解答题
如图,已知C点在圆O直径BE的延长线上,CA切圆O于A点,DC是∠ACB的平分线交AE于点F,交AB于D点.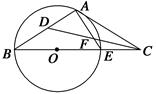
(1)求∠ADF的度数;
(2)AB=AC,求AC∶BC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC
(1)求证:BE=2AD;
(2)当AC=3,EC=6时,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在梯形ABCD中,AD∥BC,AC⊥BD,垂足为E,∠ABC=45°,过E作AD的垂线交AD于F,交BC于G,过E作AD的平行线交AB于H.求证:FG2=AF·DF+BG·CG+AH·BH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com